| Шпаргалка режимщика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Энергосистема: схемы замещения и модели элементов для расчета УР |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
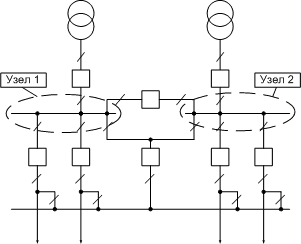
1. Узлы расчетной схемыДля любого расчета нам требуется математическая модель, отражающая поведение исследуемого объекта. В нашем случае это расчетная схема энергосистемы. Ее формирование следует начать с расстановки узлов. Где и сколько поставить узлов каждый должен решить сам, исходя из предполагаемых задач. Например, если ожидается что будет большое число расчетов с разделением шин ПС, с односторонним отключением ВЛ и т.п., то на одну ПС потребуется до 5 и более узлов. А если требуется отобразить влияние на системообразующую сеть каскада ГЭС, расположенного в соседней энергосистеме, то вполне можно обойтись и одним узлом. Вопрос проще раскрыть на примере. Предположим у нас есть ПС со схемой, изображенной на рисунке 1.1:  рис.1.1 Схема ПС Если необходимо предусмотреть возможность расчетов с раздельной работой трансформаторов по высокой стороне, то необходимо расставить
узлы так, как показано на рисунке 1.2. 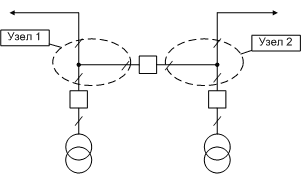 рис.1.2 Возможны расчеты с раздельной работой трансформаторов по высокой стороне Если же расчеты с раздельной работой трансформаторов по высокой стороне не предполагается, то в разделении шин высокого напряжения нет
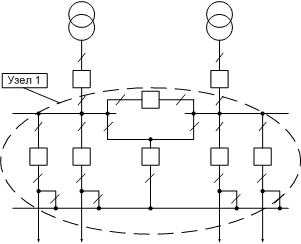
необходимости и их можно представить одним узлом, как показано на рисунке 1.3: 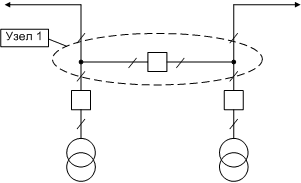 рис.1.3 Расчеты с раздельной работа трансформаторов по высокой стороне не предполагается Если же возможны расчеты и с раздельной работой трансформаторов по высокой стороне и с односторонним отключением ВЛ, то придется
вводить 3 узла, как отражено на рисунке 1.4: 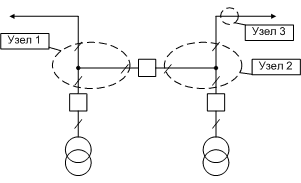 рис.1.4 Возможны расчеты и с раздельной работой трансформаторов по высокой стороне и с односторонним отключением ВЛ Аналогичный подход применяется и для низкой стороны. На рисунке 1.5 возможны расчеты с раздельной работой по низкой стороне, а на рисунке 1.6 они не предполагаются.
Для большинства ПС потребность в разделении шин при расчетах возникает крайне редко, потому обычно выделяется один узел для высокой стороны и один узел для низкой. В таком случае трансформаторы ПС в расчетной схеме будут представлены двумя параллельными ветвями. В принципе, если не предполагается расчет режима с отключением одного из трансформаторов, то их можно представить одной ветвью с эквивалентными параметрами. Но делать так не стоит потому как с одной стороны ограничения на число ветвей (как впрочем и на число узлов) в существующих расчетных программах давно снято, а с другой - наперед неизвестно какие именно ситуации придется просчитать в будущем. Таким образом, типовое представление в расчетной схеме рассматриваемой ПС будет таким, как показано на рисунке
1.7: 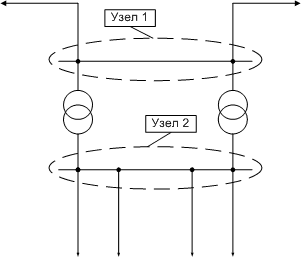 рис.1.7 Типовое представление ПС Все вышесказанное в полной мере относится и к схемам электростанций. Дополнительный нюанс, связанный со схемами электростанций - это представление генераторов. Генератор можно представить как на высокой стороне, так и на генераторном напряжении вместе с блочным трансформатором. Подход к решению вопроса как представить генератор определяется задачами, которые должны будут решаться с помощью данной расчетной модели. Например, если предполагаются расчеты, в которых генератор выдает или потребляет максимально-возможную реактивную мощность, то он должен быть представлен на генераторном напряжении для корректного учета располагаемой реактивной мощности, приведенной к стороне высокого напряжения, величина которой зависит от потерь в блочном трансформаторе. После расстановки узлов необходимо определить параметры связывающих их линий. Здесь возможны варианты:
В 1-м случае необходимо использовать ветви с нулевым сопротивлением. Сейчас большинство расчетных программ умеют корректно обрабатывать такую величину. Если же в каких-то частных случаях такой подход не приемлем, то нужно использовать величину близкую к нулю, например Z=0+j0.01 2. Линий электропередачДля моделирования линии электропередач применяется П-образная схема замещения: 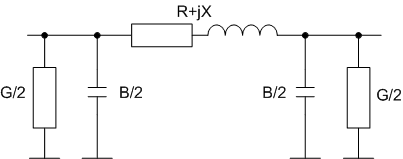 рис.2.1 П-образная схема замещения Значения R [Ом], X [Ом], B [См] определяются длиной
L [км] линии между соседними узлами расчетной схемы и значениями удельных параметров r0 [Ом/км],
x0 [Ом/км], b0 [См/км]:
R=r0L; X=x0L; B=b0L (2.1)
Поскольку П-образная схема, в которой емкостная и активная
проводимости линий сосредоточены в ее концах, не дает возможности точно
отобразить соотношение между токами и напряжениями на линии, при больших длинах
линий ее приходится разбивать на участки до 200-300 км или вводить поправочные
коэффициенты:
R=r0LKr; X=x0LKx; B=b0LKC (2.2)
Значения поправочных коэффициентов для линий длиной от 300 до 500-600 км
вычисляются по формулам: 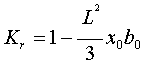
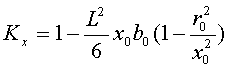
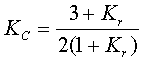 (2.3) (2.3)при малых длинах линий эти коэффициенты близки к единице. Активная проводимость на землю G для ВЛ определяется потерями на корону, а для КЛ - потерями в изоляции кабеля. Потери на корону в основном невелики и сильно зависят от погоды. При измороси они многократно больше, чем в сухую погоду. Но из-за неопределенности этой величины ее как правило не учитывают. При необходимости потери на корону можно учесть используя G, либо включением дополнительной активной нагрузки в узле с постоянным значением или зависимым от напряжения в узле.
Для КЛ напряжением 110 кВ и выше необходимо учитывать потери в изоляции кабеля.
Они определяются по формуле:
G=Btgδ (2.4)
При этом tgδ определяется по данным завода-изготовителя и обычно находиться в пределах от 0.003 - 0.006.
Примеры определения параметров линии.
R=r0L=0.121*200=24.2 [Ом]; X=x0L=0.435*200=87.0 [Ом]; B=b0L=2.60*10-6*200=520*10-6 [См]. В исходных данных какая-либо информация о погоде в месте прохождении линии
отсутствует, поэтому G линии примем равным 0.
Пример 2.2 Исходные данные. Номинальное напряжение U=500 кВ, длина L=500 км, провод 3*АС-300 (3 провода в фазе). Расчет. Из таблицы 7.6 "Расчетные данные ВЛ 220 - 1150 кВ со сталеалюминевыми проводами (на 100 км)" справочника [4] в пересчете на 1 км находим r0=0.034 Ом/км, x0=0.310 Ом/км, b0=3.97*10-6 См/км. Так как длина линии 500 км, параметры линии необходимо определять по формулам (2) c учетом поправочных коэффициентов, определяемых по формулам (2.3): 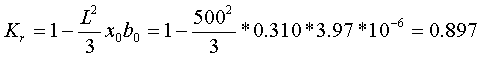 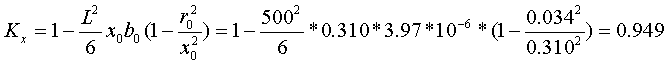 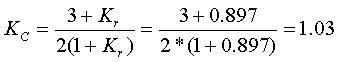 R=r0LKr=0.034*500*0.897=15.2 [Ом]; X=x0LKx=0.310*500*0.949=147 [Ом]; B=b0LKC=3.97*10-6*500*1.03=2040*10-6 [См]. В исходных данных какая-либо информация о погоде в месте прохождении линии отсутствует, поэтому G линии примем равным 0. В приведенных примерах все результаты расчетов даны с точностью до 3-х значащих цифр, т.к. именно с такой точностью они указаны в справочнике. 3. Трансформаторы1. двухобмоточные трансформаторыДля двухобмоточных трансформаторов и автотрансформаторов, когда не используется
третья обмотка, используется Г-образная схема замещения: 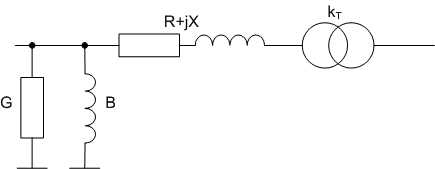 рис.3.1.1 Г-образная схема замещения Параметры Г-образной схемы замещения определяются по следующим формулам:
Условные обозначения:
Пример определения параметров двухобмоточного трансформатора. Пример 3.1.1 Исходные данные. Тип трансформатора ТДЦ-80000/110. Расчет. Трансформатор двухобмоточный, поэтому применяем Г-образную схему замещения (рис.3.1.1) Из таблицы 5.13 "Трехфазные двухобмоточные трансформаторы 110 кВ" справочника [6] находим Sном=80 МВА, UВН=121 кВ, UНН=10.5 кВ, uk=10.5 %, Pk=310 кВт, Pхх=70 кВт, Iхх=0.6 %. Все расчетные величины будем приводить к стороне ВН. По формулам (3.1.1) определяем: 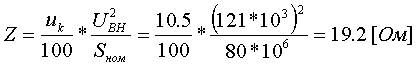 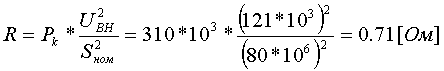 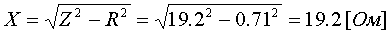 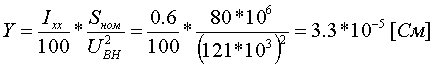 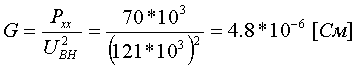 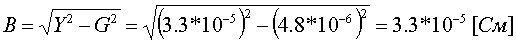 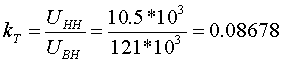 2. автотрансформаторы и трехобмоточные трансформаторыДля автотрансформаторов и трехобмоточных трансформаторов используется схема замещения в виде трехлучевой звезды:
 рис.3.2.1 Трехлучевая схема замещения Параметры данной схемы замещения определяются по следующим формулам: G [См] и B [См] - по таким же формулам, как и для двухобмоточного трансформатора:
Полные сопротивления Z [Ом] определяются по формулам: 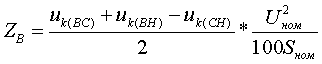 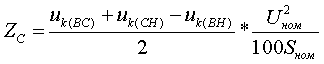 (3.2.2) (3.2.2)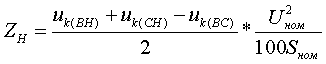
В случае если известны все три значения потерь КЗ между парами обмоток, то активные сопротивления
R [Ом] определяются по формулам: 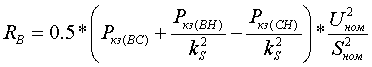 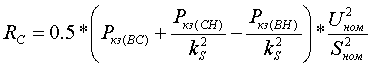 (3.2.3) (3.2.3)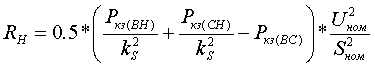 Если в каталожных данных указывается только значение максимальных потерь КЗ, то активные сопротивления определяются следующим образом:
По найденным Z и R находятся индуктивные сопротивления X [Ом]: 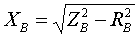 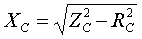 (3.2.6) (3.2.6)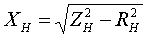 Знак у индуктивного сопротивления X принимается такой же как у соответствующего ему полного сопротивления Z, определяемого по формулам (3.2.2). При наличии вольтодобавочного трансформатора, включенного в нейтраль автотрансформатора, сопротивления
корректируются в соответствии с формулами (при условии, что они были приведены к стороне ВН):
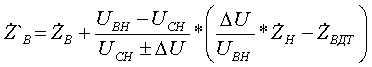  (3.2.7) (3.2.7)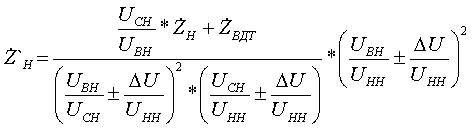 Примечание: Формулы (12) для учета ВДТ являются переработанными формулами (2.27)-(2.30) методических указаний [3]. К сожалению, найти указанные формулы в какой-либо другой справочной литературе не удалось. Коэффициенты трансформации определяются по формулам:
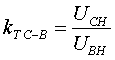
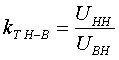 (3.2.8) (3.2.8)Если производится добавка линейного (междуфазного) напряжения, то угол добавочного напряжения в формулах (3.2.11), (3.2.12) необходимо изменить в соответствии с фактическим углом между основным и добавочным напряжениями. Условные обозначения:
Примеры определения параметров автотрансформаторов. Пример 3.2.1 Исходные данные. Тип автотрансформатора АТДЦТН-250000/330/150. Автотрансформатор оснащен РПН ±6x2 % на стороне СН. Расчет. Предположим, что требуется явное представление всех обмоток автотрансформатора. Для этого необходима трехлучевая схема замещения (рис.3.2.1) Из таблицы 5.20 "Трехфазные и однофазные автотрансформаторы 330 кВ" справочника [6] находим Sном=250 МВА, UВН=330 кВ, UСН=158 кВ, UНН=10.5 кВ, uk(ВС)=10.5 %, uk(ВН)=54 %, uk(СН)=42 %, Pk(ВС)=660 кВт, Pk(ВН)=490 кВт, Pk(СН)=400 кВт, Pхх=165 кВт, Iхх=0.5 %, мощность обмотки НН составляет 40 % номинальной мощности АТ. Все расчетные величины будем приводить к стороне ВН. По формулам (3.2.1) и (3.2.2) определяем G, B и Z: 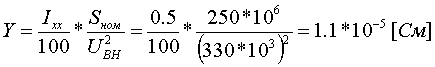 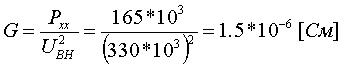  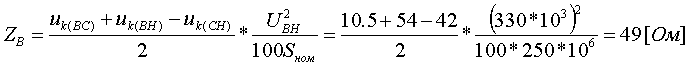 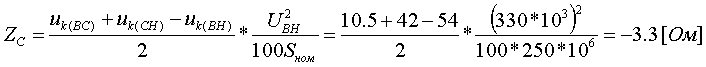 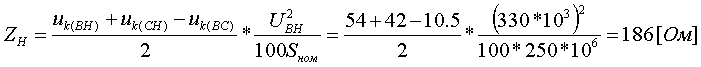 В исходных данных указано, что мощность обмотки НН составляет 40 % от номинальной мощности АТ, поэтому: kS=SНН/Sном=0.4 Активное сопротивления АТ определяем по формулам (3.2.3), т.к. даны потери КЗ Pk(ВС), Pk(ВН), Pk(СН): 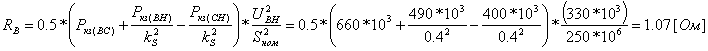 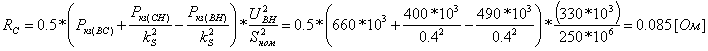 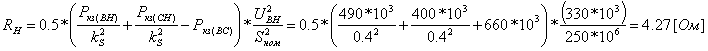 По формулам (3.2.6) находим индуктивные сопротивления X [Ом]: 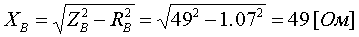 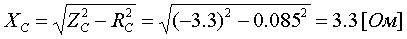 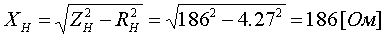 Учитывая, что ZС отрицательно, окончательно принимаем XС=-3.3 [Ом]. По условию задачи РПН, установлен на стороне СН, поэтому при изменении положения анцапфы будет изменяться только коэффициент трансформации между СН и ВН kT С-В, коэффициент трансформации между НН и ВН kT Н-В при изменении положения анцапфы меняться не будет. В связи с этим kT Н-В необходимо определять по формуле (3.2.8): 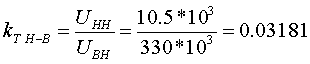 Учитывая, что значение kT С-В определяется текущим номером анцапфы, определим только его крайние значения. Для этого необходимо определить добавку напряжения ΔU в крайних положениях РПН, принимая во внимание, что шаг ступени указан относительно стороны СН: 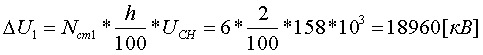 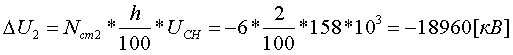 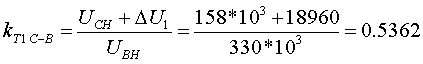 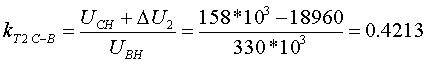 Пример 3.2.2 Исходные данные. Тип автотрансформатора АТДЦТН-250000/220/110. Расчет. Будем использовать трехлучевую схему замещения (рис.3.2.1) Из таблицы 5.18 "Трехфазные трехобмоточные трансформаторы и автотрансформаторы 220 кВ" справочника [6] находим Sном=250 МВА, UВН=230 кВ, UСН=121 кВ, UНН=38.5 кВ, uk(ВС)=11.5 %, uk(ВН)=33.4 %, uk(СН)=20.8 %, Pk(ВС)=520 кВт, Pхх=145 кВт, Iхх=0.5 %, мощность обмотки НН составляет 50 % номинальной мощности АТ. Все расчетные величины будем приводить к стороне ВН. По формулам (3.2.1) и (3.2.2) определяем G, B и Z: 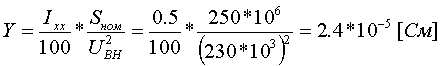 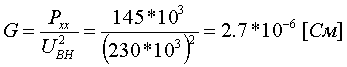 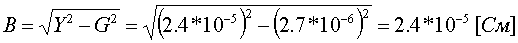 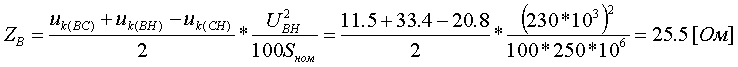 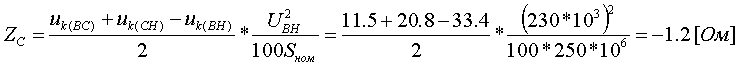 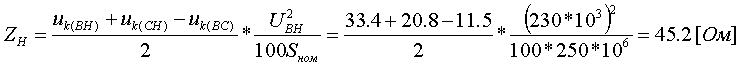 В исходных данных указано, что мощность обмотки НН составляет 50 % от номинальной мощности АТ, поэтому: kS=SНН/Sном=0.5 Активное сопротивления АТ определяем по формулам (3.2.5), т.к. даны только максимальные потери КЗ Pk(ВС): 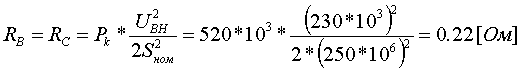 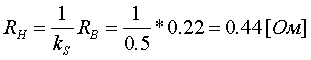 По формулам (3.2.6) находим индуктивные сопротивления X [Ом]: 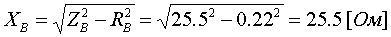 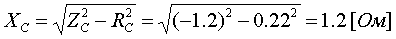 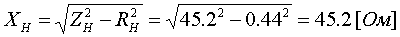 Учитывая, что ZС отрицательно, окончательно принимаем XС=-1.2 [Ом]. Коэффициенты трансформации будем определять по формулам (3.2.8), т.к. рассматриваемый АТ не оснащен средствами для регулирования напряжения: 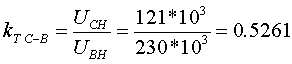 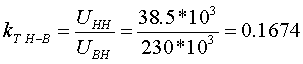 Пример 3.2.3 Исходные данные. Автотрансформатор из примера 3.2.2 дополнительно оборудован вольтодобавочным трансформатором ВРТДНУ-240000/35/35. Расчет. Рассчитаем параметры ВДТ по формулам (3.1.1) и определим итоговые параметры автотрансформатора, работающего совместно с ВДТ, опираясь на формулы (3.2.7) и рассчитанные в примере 3.2.2 значения. Для расчета по формулам (3.2.7) требуется 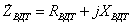 . Для его определения из таблицы 5.23
"Последовательные регулировочные трансформаторы" справочника [6] находим
Sном=240 МВА, Uвозб=38.5 кВ,
Uрег=ΔU=+24.9 ÷ -26.2 кВ, uk=11.1 - 0 - 11.3 %,
Pk=178 кВт. . Для его определения из таблицы 5.23
"Последовательные регулировочные трансформаторы" справочника [6] находим
Sном=240 МВА, Uвозб=38.5 кВ,
Uрег=ΔU=+24.9 ÷ -26.2 кВ, uk=11.1 - 0 - 11.3 %,
Pk=178 кВт.Определим сопротивление ВДТ при крайних положениях анцапф по формулам (3.1.1): 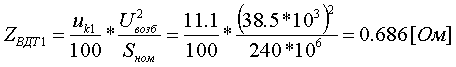 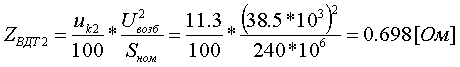 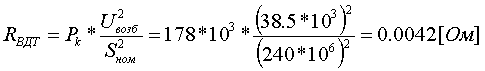 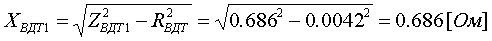 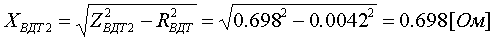 Запишем полученные параметры ВДТ и АТ в комплексном виде: 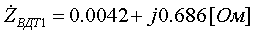 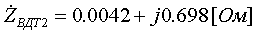 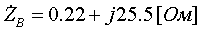 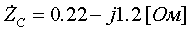 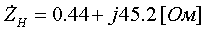 По формулам (3.2.7) окончательно определяем: 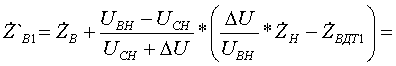 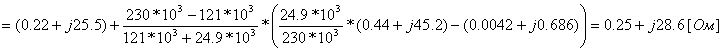  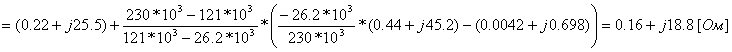 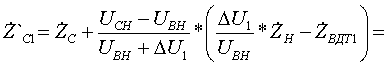 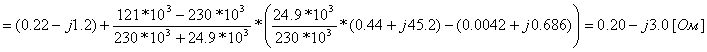 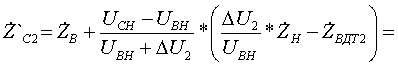 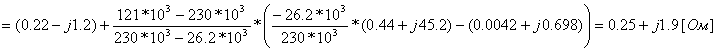 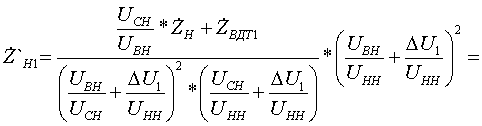 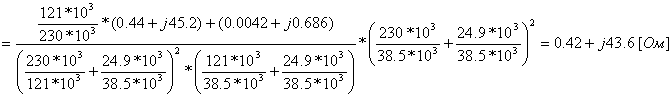 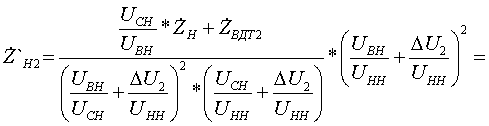 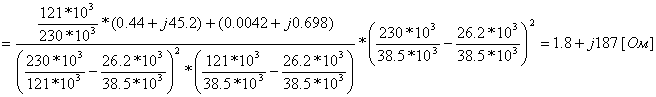
По формуле (3.2.9) определяем kT В-Н при крайних положениях анцапф (знак минус уже учтен в ΔU): 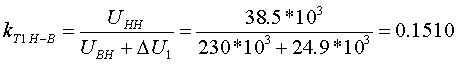 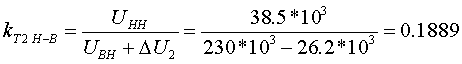 По формуле (3.2.10), учитывая, что знак минус уже учтен в ΔU, определяем kT C-Н при крайних положениях анцапф: 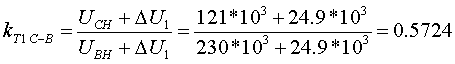 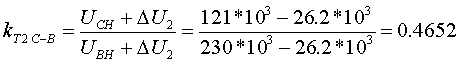 Для анализа полученные результаты сведем в таблицу:
3. трансформаторы с расщепленной на 2 части обмоткойДля трансформаторов с расщепленной на 2 части обмоткой низшего напряжения применяется схема замещения в виде трехлучевой звезды:
 рис.3.3.1 Схема замещения трансформатора с расщепленной на 2 части обмоткой низшего напряжения Для трансформаторов с расщепленной обмоткой специфическими параметрами являются: 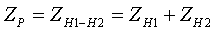 (3.3.1) (3.3.1)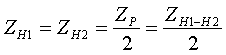 (3.3.2) (3.3.2)- сквозное сопротивление Zскв=ZВ-Н, равное сопротивлению между выводами обмотки высокого напряжения и объединенными (запараллелеными) ветвями расщепленной обмотки низшего напряжения; - коэффициент расщепления КР, равный отношению ZР к Zскв: 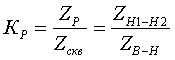 (3.3.3) (3.3.3)Для трехфазных трансформаторов КР=3.34 ÷ 3.64; при отсутствии точных данных принимается КР=3.5. Для трехфазной группы однофазных трансформаторов КР=4. Параметры схемы замещения определяются по следующим формулам: G [См] и B [См] - по таким же формулам, как и для двухобмоточного трансформатора:
Выбор формул для нахождения Z[Ом] определяется составом исходных данных (все сопротивления
должны быть приведены к обмотке ВН по формуле
Как видно из формул, для трехфазной группы однофазных трансформаторов ZН1=ZН2=2ZВ-Н; ZВ=0. Активные сопротивления R[Ом] находятся по формулам:
По найденным Z и R определяются X[Ом]:
Коэффициент трансформации определяется таким же образом, как для двухобмоточного трансформатора: 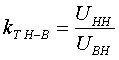 (3.3.13) (3.3.13)Пример определения параметров двухобмоточного трансформатора c расщепленной на 2 части обмоткой. Пример 3.3.1 Исходные данные. Тип трансформатора ТРДЦН-160000/220. Расчет. Трансформатор двухобмоточный с расщепленной обмоткой, поэтому применяем трехлучевую схему замещения (рис.3.3.1). Из таблицы "Трансформаторы с расщепленной на 2 части обмоткой низшего напряжения" находим Sном=160 МВА, UВН=230 кВ, uк.В-Н=12.5 %, uк.В-Н1(Н2)=23.0 %, uк.Н1-Н2=42.0 %, КР=3.360, Pk=525 кВт, Pхх=140 кВт, Iхх=0.6 %. Примем UНН=6.6 кВ. Все исходные и расчетные величины приведены к стороне ВН. По формулам (3.3.4) определяем: 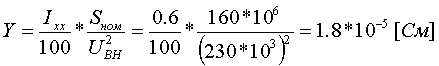 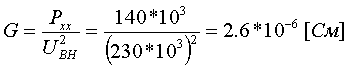 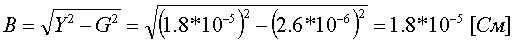 Для определения Z будем использовать ZВ-Н и ZН1-Н2 (п. с): 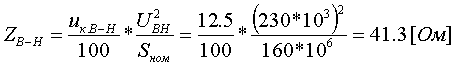 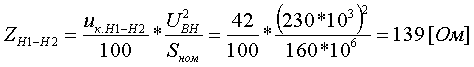 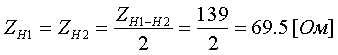 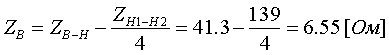 По формулам (3.3.11) определяем R: 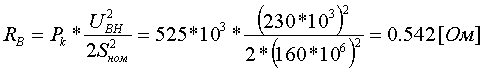 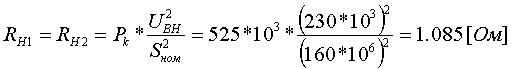 По формулам (3.3.12) определяем X: 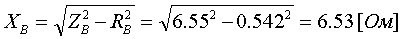 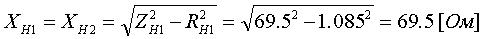 По формуле (3.3.13) определяем kТ Н-В: 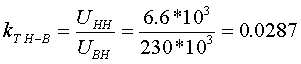 4. трансформаторы с расщепленной на 3 части обмоткойДля трансформаторов с расщепленной на 3 части обмоткой низшего напряжения применяется схема замещения в виде четырехлучевой звезды:
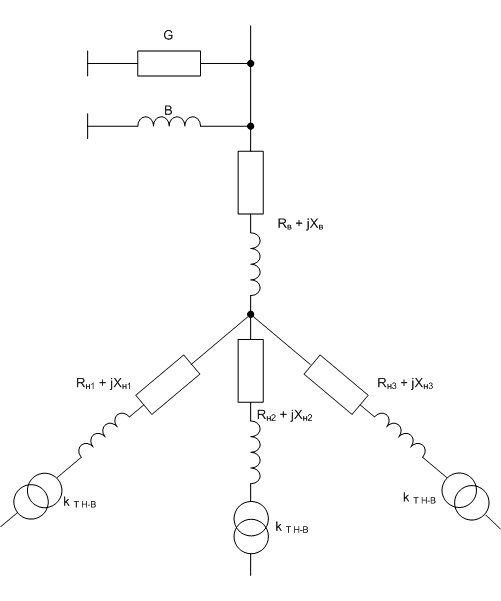 рис.3.4.1 Схема замещения трансформатора с расщепленной на 3 части обмоткой низшего напряжения Параметры схемы замещения определяются по следующим формулам: G [См] и B [См] - по таким же формулам, как и для двухобмоточного трансформатора:
Сопротивления трансформатора Z[Ом] определяются по формулам:
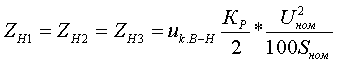 (3.4.2) (3.4.2) (3.4.3) (3.4.3)Коэффициент расщепления для трехфазной группы однофазных трансформаторов с расщепленной на 3 части обмоткой низшего напряжения КР=6. Как видно из формул, для трехфазной группы однофазных трансформаторов ZН1=ZН2=ZН3=3ZВ-Н; ZВ=0. Активные сопротивления R[Ом] находятся по формулам:
По найденным Z и R определяются X[Ом]:
Коэффициент трансформации определяется таким же образом, как для двухобмоточного трансформатора: 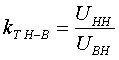 (3.4.6) (3.4.6)5. автотрансформаторы с расщепленной обмоткойДля автотрансформаторов с расщепленной на 2 части обмоткой низшего напряжения применяется схема замещения, изображенная на рис. 3.5.1:
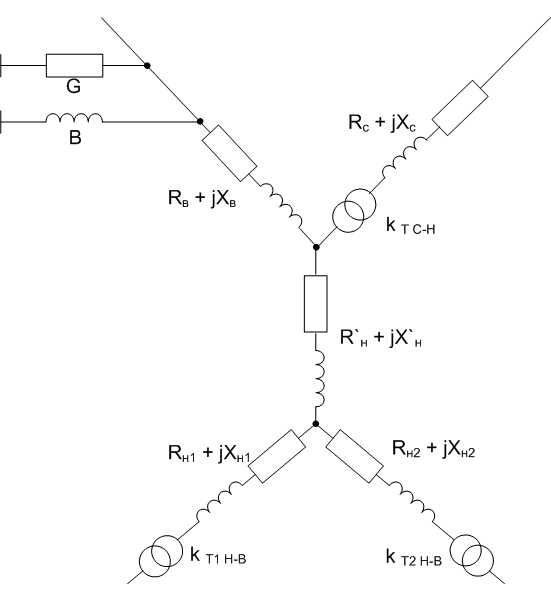 рис.3.5.1 Схема замещения автотрансформатора с расщепленной на 2 части обмоткой низшего напряжения Параметры схемы замещения определяются по следующим формулам: G [См] и B [См] - по таким же формулам, как и для двухобмоточного трансформатора:
Полные сопротивления Z [о.е.] определяются по формулам: 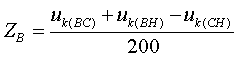 (3.5.2) (3.5.2)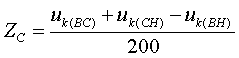 (3.5.3) (3.5.3)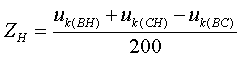 (3.5.4) (3.5.4)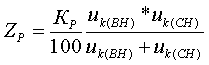 (3.5.5) (3.5.5)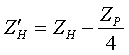 (3.5.6) (3.5.6)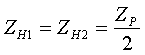 (3.5.7) (3.5.7)где uk(ВН) и uk(СН) получены при включенных параллельно обмотках НН. Перевод из относительных величин в именованные осуществляется по стандартной формуле: 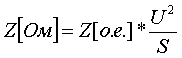 (3.5.8) (3.5.8)Активные сопротивления определяются таким же образом, как и для обычного автотрансформатора (см. формулы (3.2.3÷3.2.5)); R` принимается равным 0 (R`=0); RН1=RН2=2RН. По найденным Z и R определяются X[Ом]:
Знак у индуктивного сопротивления X принимается такой же как у соответствующего ему полного сопротивления Z. Коэффициенты трансформации определяются таким же образом, как и для обычного автотрансформатора (см. формулы (3.2.8÷3.2.12)) 4. НагрузкаМоделирование нагрузки при расчетах установившегося режима производиться с использованием статических характеристик нагрузки
СХН. Данные характеристики показывают зависимость нагрузки от напряжения и частоты в месте подключения нагрузки.
Существующая зависимость нагрузки от частоты хорошо моделируется линейной функцией.
Все варианты задания нагрузки обобщены в виде:
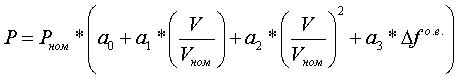 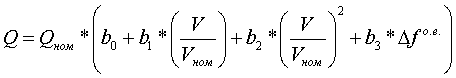 где a0, a1, a2, a3, b0, b1, b2, b3 - коэффициенты; V - расчетное напряжение; Vном - номинальное напряжение; Δf - отклонение частоты, о.е. Примечание: Данная форма уравнений СХН принята в отечественной практике. В зарубежных расчетных программах характеристики СХН определяются через показатель степени у отклонения напряжения и частоты. Подробней об этом см. описание соответствующих программ. Условие P=Pном и Q=Qном при V=Vном и Δf=0 выполняется, когда a0+a1+a2=1 и b0+b1+b2=1. Нагрузка, представленная в виде постоянных сопротивлений реализуется a0=0, a1=0, a2=1 и b0=0, b1=0, b2=1; в виде постоянного тока - a0=0, a1=1, a2=0 и b0=0, b1=1, b2=0; в виде постоянной мощности - a0=1, a1=0, a2=0 и b0=1, b1=0, b2=0. Различие характеристик изображено на рисунке: 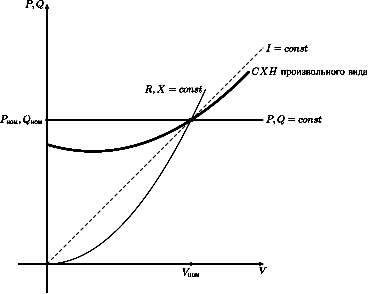 рис.4.1 Статических характеристики нагрузки Для типовой нагрузки применяют следующие СХН:
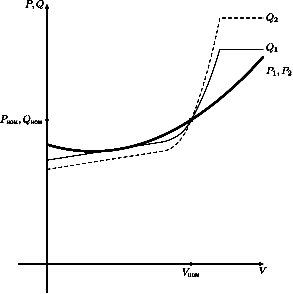 рис.4.2 Стандартные статические характеристики нагрузки по напряжению 5. Реакторы и батареи конденсаторов
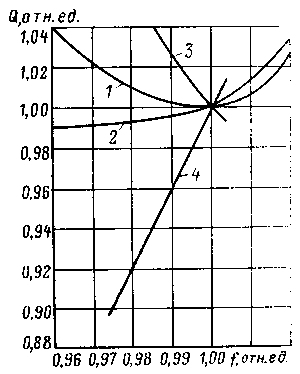
Пример определения параметров шунтирующего реактора и БСК. 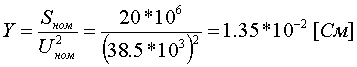 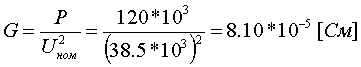 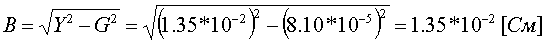 Пример 5.2 БСК: Установленная мощность Q=52 МВАр, номинальное напряжение Uном=110 кВ. Из таблицы 5.32 "Шунтовые конденсаторные батареи 6 - 110 кВ" справочника [6] находим, что при номинальном напряжении мощность, выдаваемая батареей Qб равна 36.8 МВАр. По формуле (5.3) находим: 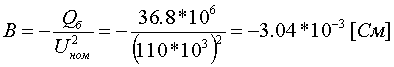 Следует отметить, что моделирование реакторов и конденсаторных батарей должно осуществляться именно пассивными элементами, а не инъекциями мощности. В этом плане весьма показательна приведенная ниже таблица, полученная по данным рассмотренных примеров: Зависимость мощности, генерируемой шунтирующим реактором и БСК от напряжения
6. Генераторы и синхронные компенсаторы, балансирующий узелПри расчетах установившегося режима для отображения генераторов используют одну из двух моделей: PQ или PU (вместо Q и U возможно использование некоторой ЭДС E за хгенератора, определяемым по специальным правилам, но такой подход не нашел широкого практического применения).В первом случае в исходных данных узла, отображающего генератор (далее - генераторный узел) указывается генерируемая активная P и реактивная Q мощности. При этом такой генератор не учувствует в поддержании напряжения в узле. Как правило, таким образом моделируются малоответственные небольшие генераторы, установленные у потребителя и фактический режим работы которых оказывает незначительное влияние на результат решения рассматриваемых задач (хотя и их рекомендуется представлять по модели PU).
Применение второй модели - PU - является наиболее эффективным и отражает фактическое положение дел, т.к.
большинство генераторов оборудовано системой автоматической регулировки возбуждения АРВ, обеспечивающей в
установившемся режиме практически неизменное напряжение на шинах генератора или на стороне высокого напряжения блочного
трансформатора, через который генератор связан с энергосистемой. При этом погрешность, вносимая неучетом существующей
зависимости U=f(P,Q) минимальна.  рис.6.1 Типовая диаграмма мощности К сожалению, в большинстве программ для расчета установившегося режима нет возможности задания зависимости Q=f(P). Вместо этого предлагается только указать Qmin и Qmax ("вилка" по Q). В такой ситуации для всех генераторов задается минимальная и максимальная величина генерации реактивной мощности, определяемая по диаграмме мощности. Учет фактических ограничений производиться только для влияющих на решение конкретной задачи генераторов путем сужения "вилки" по Q в соответствии с текущей генерацией активной мощности P. В ходе расчета может случиться, что генерируемая реактивная мощность Q достигнет одной из границ Qmin или Qmax. В таком случае генераторный узел будет автоматически переведен с модели PU на модель PQ, после чего он перестанет "поддерживать" заданное напряжение U в узле. Если же в дальнейших расчетах потребная для поддержания напряжения U генерируемая реактивная мощность Q вновь окажется внутри "вилки" по Q, то генераторный узел будет обратно переведен на модель PU. Учет зависимости генерации активной мощности P от частоты f производится через статизм генератора σ= (Δfо.е./ΔPо.е.)*100 %, который по действующим нормам должен быть ~5 %. Учет зоны нечувствительности регулятора скорости, как правило, не производится, т.к. текущее положение регулирующих органов во многом величина случайная и мало предсказуемая. А с учетом того, что в энергосистеме присутствует большое число генераторов, то на "общем фоне" зона нечувствительности отдельного генератора "теряется". Учет зависимости генерации реактивной мощности Q от частоты f в основном определяется характеристиками АРВ
(ее зависимость от изменения хгенератора незначительна). Так же от частоты f зависит и "вилка"
по Q, т.к. при неизменном токе ротора if (т.е. при выходе генератора на одно из ограничений
Qmin или Qmax) ЭДС E, генерируемая в статоре током возбуждения, пропорциональна
частоте вращения ротора. Моделирование синхронных компенсаторов осуществляется аналогично моделированию генераторов, при этом P=0. Балансирующий узел - это узел за счет которого при расчетах установившегося режима без изменения частоты в расчетной схеме поддерживается баланс между генерацией и потреблением. Для работы в таком режиме в узле должен быть зафиксирован вектор напряжения, т.е. U и φ. Таким образом генерация активной и реактивной мощности в таком узле в ходе расчета могут изменяться программой самостоятельно для обеспечения баланса. Как правило, балансирующий узел назначается и базовым узлом, т.е. отсчеты углов всех векторов напряжения φ осуществляются относительно него. В связи с этим угол напряжения в балансирующем узле принимают равным нулю φ=0. В качестве балансирующего узла, как правило, назначается самый мощный генератор в энергосистеме или какой-либо узел в соседнем объединении. Выбор определяется тем, за счет каких источников фактически производиться ликвидация небалансов мощности, вызываемых небольшими колебаниями нагрузки. При проведении расчетов установившегося режима с учетом изменения частоты баланс между генерацией и потреблением устанавливается без участия балансирующего узла за счет СХН нагрузки и статизма генераторов σ. В этом случае балансирующий узел выполняет только роль базового узла.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последние изменение 16.02.2007 Сергей Мотовилов |
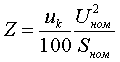
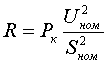
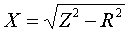
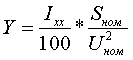
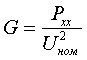
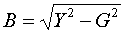
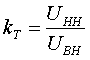
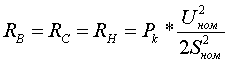 (3.2.4)
(3.2.4)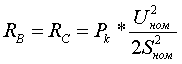
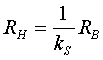 (3.2.5)
(3.2.5)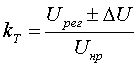
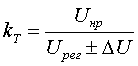 (3.2.9)
(3.2.9)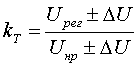 (3.2.10)
(3.2.10)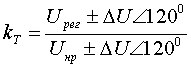 (3.2.11)
(3.2.11)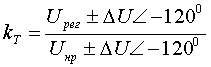 (3.2.12)
(3.2.12)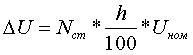 (3.2.13)
(3.2.13)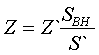 и представлены в именованных единицах
и представлены в именованных единицах 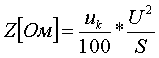 ):
):
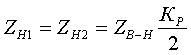 (3.3.5)
(3.3.5)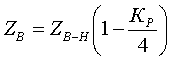 (3.3.6)
(3.3.6)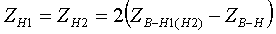 (3.3.7)
(3.3.7)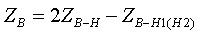 (3.3.8)
(3.3.8)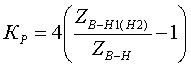 (3.3.9)
(3.3.9)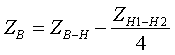 (3.3.10)
(3.3.10)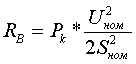
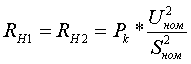
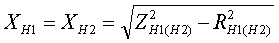
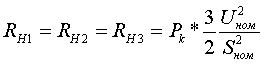
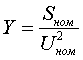
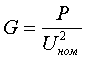
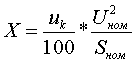 (5.2)
(5.2)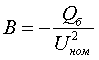 (5.3)
(5.3)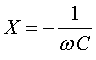 (5.4)
(5.4)