Новый алгоритм создания динамических эквивалентов больших энергосистем
(перевод статьи “A Novel Algorithm for Dynamic Equivalents of Large Power Systems”)
X. Lei, O. Ruhle – Siemens AG, Германия;
B. Kulicke – Technical University of Berlin, Германия;
Y. Han – Tsinghua University Beijing, Китай.
В рыночных условиях вопрос эквивалентирования энергосистем становится крайне острым.
Данная статья представляет новый алгоритм снижения размерности схемы замещения большой энергосистемы,
который основан на идее динамической когерентности. Генераторы в эквивалентируемой подсистеме,
при воздействии на нее сигналом "белый шум", реагируют независимо от типа и места приложения возмущения.
Когерентные в переходных процессах генераторы с высокой точностью выявляются благодаря использованию
корреляционного анализа. Динамический эквивалент может быть получен автоматически с помощью расчетной
программы, в которой описана нелинейная модель сложной системы и в которую включен предлагаемый алгоритм.
Расчеты по данному методу выполняются во временной области и не предполагают какой-либо линеаризации системы.
В статье приведен пример расчетов для реальной энергосистемы. Полученный результат подтверждает эффективность
представленного метода снижения размерности схемы замещения большой энергосистемы.
Ключевые слова.
Динамический эквивалент, нелинейная модель, динамическая когерентность, взаимная корреляция, "белый шум", NETOMAC.
1. Введение
Конкурентный рынок и приватизация в энергетической сфере значительно изменили взаимоотношения между электростанциями, передающими и распределяющими организациями. В новых условиях они переориентировались на получение максимальной прибыли, что значительно усложнило обмен между ними детализированным описанием энергосистем, так как такая информация стала рассматриваться как сугубо конфиденциальная. В то же время, возросшие требования к режимам работы энергообъединения требуют тщательного анализа как текущих режимов, так и прошедших. При этом должны быть проработаны такие вопросы как статическая и динамическая устойчивость, согласование работы систем централизованной и локальной автоматики и т.д. Таким образом, проблематика создания эквивалентов для большой объединенной системы, части которой находятся в собственности множества различных организаций, становиться крайне острой.
С другой стороны, при проведении анализа, общей практикой является представление частей энергосистемы некоторым эквивалентом, например модели для исследования динамики энергосистемы, анализ уровней напряжения и т.д. Кроме того, в связи с ограничением используемых программ (подобных Real-Time-Digital-Simulator (RTDS) или Electromagnetic Transients Program for DC-application (EMTDC)) на размерность модели, пользователи вынуждены прибегать к эквивалентированию. Так же, в ряде случаев, эквивалентированная модель может упростить вычисления и снизить затраты времени на проведения исследований. В зависимости от решаемых задач, эквивалентные модели могут быть сформированы либо путем статического, либо путем динамического эквивалентирования.
Исследования по эквивалентированию больших энергосистем проводятся уже около 30 лет. Различные алгоритмы и процедуры были проанализированы в литературе [1-3]. Некоторые из этих процедур были реализованы [4]. Другие находятся в стадии разработки. Эти методы обычно основаны на линеаризации рассматриваемой системы и существуют как самостоятельный продукт. Из-за высоких требований к предварительной ручной подготовке данных, только очень небольшое число алгоритмов динамического эквивалентирования доступно для практического применения. Как результат этого, динамическое эквивалентирование часто выполняется с использованием эвристических методов. Дополнительно, линейные методы не могут точно воспроизвести сложную динамику системы особенно при больших возмущениях. Полученный с использованием линейного метода эквивалент обеспечивает требуемое поведение в условиях малого сигнала и не может гарантировать приемлемое поведение при большом возмущении.
Цель данной статьи – представить нелинейный подход для эквивалентирования больших и очень больших энергосистем. В данном алгоритме используется корреляционный анализ для определения когерентных генераторов. Внесение возмущения в виде "белого шума" в эквивалентируемую подсистему приводит к возбуждению генераторов в ней. Причем реакция генераторов не зависит от типа и места внесения возмущения. Используя корреляционный анализ, определяется корреляция между движением роторов генераторов и с высокой точностью выявляются когерентные генераторы. Агрегирование когерентных генераторов и создание эквивалента окружающей их сети приведет к автоматическому созданию динамического эквивалента, отражающего нелинейную природу эквивалентируемой системы. Кроме того, предлагаемый алгоритм учитывает влияние систем автоматического регулирования генераторов. Возбудители и регуляторы скорости генераторов в когерентной группе генераторов заменяются эквивалентным возбудителем и регулятором скорости. Их параметры определяются таким образом, чтобы минимизировать различие в поведение полной модели и ее эквивалента.
Остальная часть статьи организована следующим образом: в разделе 2 представляется базовая идея алгоритма, приводится описание подхода
к моделированию энергосистем и дается краткий обзор корреляционного анализа. В заключение 2-го раздела описывается вся процедура
эквивалентирования, разбитая на 4 шага. В разделе 3 демонстрируется пример изучения большой энергосистемы. Выводы приведены в
разделе 4, а ссылки на литературу расположены в разделе 5.
2. Алгоритм
2.1 Моделирование энергосистем.
Сложная нелинейная модель энергосистемы может быть описана в виде системы дифференциально-алгебраических уравнений,
получаемых путем связывания моделей генераторов, нагрузки и других устройств таких как регуляторы через уравнения сети.
Начиная с уравнений движения n-того генератора, пренебрегая демпфированием, математическая модель энергосистемы
может быть описана как:
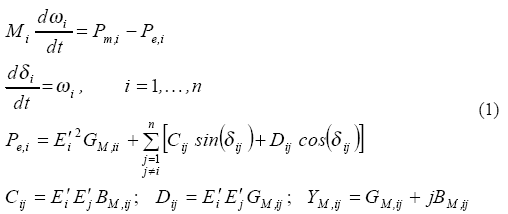
где:
δi – угол ротора
ωi – угловая скорость ротора
Mi – постоянная инерции
Pm,i – механическая мощность
Pe,i – электрическая мощность
E`i – ЭДС за переходным сопротивлением
YM – матрица проводимости генератора
Для описания такой нелинейной системы используется программа NETOMAC, описанная в [5-6]. В ней дифференциальные уравнения преобразуются в системы алгебраических уравнений, решаемых хорошо известным трапецеидальным методом. Во временной области программа выдает мгновенное значение модуля подобно программе EMTDC/EMTP, так же она обладает модулем анализа устойчивости подобно программе PSS/E. Для работы в частотной области программа NETOMAC снабжена модулем частотного анализа и модулем анализа собственных чисел. Дополнительно, она включает в себя оптимизационный/идентификационный режим [7] для решения различных оптимизационных задач и задач идентификации параметров. Недавно новый метод автоматического динамического эквивалентирования был так же интегрирован в программу NETOMAC. Одним из значительных преимуществ программы NETOMAC является то, что такой широкий спектр задач использует единую оболочку и базу данных без необходимости проведения какой-либо конвертации между модулями.
В программе NETOMAC все процедуры, относящиеся к моделированию системы, проведению расчетов, выполнению эквивалентирования
и верификации результатов реализованы в единой оболочке и используется общая база данных. Ни одна из задач не требует конвертации
данных. Как только получен эквивалент, сразу же может быть проведена верификация как во временной, так и в частотной области с помощью
широкого спектра модулей анализа, доступных в программе.
2.2. Корреляционный анализ
Для идентификации когерентных генераторов исследуется подобие графиков изменения параметров генераторов с использованием корреляционного анализа [9]. В результате возмущения генераторы в системе возбуждаются. Следовательно, отклонение скорости генераторов, описанное (1) может хорошо показать динамические характеристики системы после возмущения. Для идентификации когерентных генераторов с помощью корреляционного анализа используется отклонение скорости ωi(l) (i=1,…, n). Далее рассматриваются принципы корреляционного анализа, т.к. они служат основой предлагаемого алгоритма.
Предположим, что полная энергия E изменяющихся во времени графиков скорости ωi(l) и ωj(l)
(l=-∞ … +∞) генераторов i и j вычисляется соответственно как:
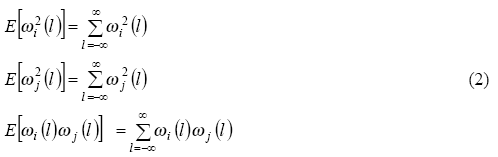
Очевидно, что энергии E[ω2i(l)] и E[ω2j(l)] константы для каждого отдельно взятого отклонения скорости и E[ωi(l) ωj(l)] – величина, показывающая корреляцию между двумя сигналами.
Полная ошибка энергии ξ2 между двумя сигналами ωi(l) и αωj(l) определяется как:

где α неслучайная константа. ξ2 достигает минимума как только выполнится условие

из которого величина α получается равной

Подставляя (5) в (3), минимум ξ2 определяется как
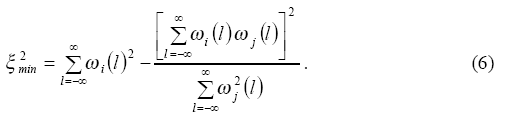
где ξ2min показывает, что сигналы ωi(l) и αωj(l) весьма подобны. Более того, для определения степени подобия сигналов подходит относительная ошибка энергии
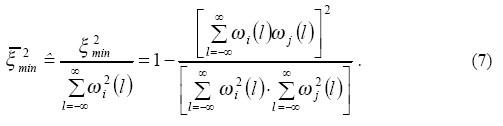
Введя отношение
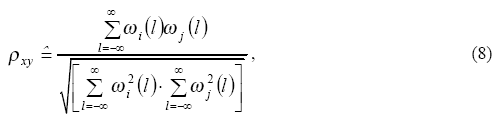
то, как следует из неравенства Шварца (неравенство Буняковского – прим. пер.)
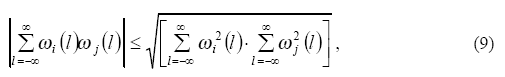
коэффициент корреляции ρij, показывающий степень подобия графиков двух сигналов, может быть определен в диапазоне

где, как отмечено в (2), Eij и rij определяются как
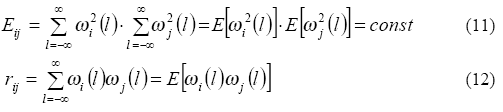
Из (10) и (11) легко понять, что коэффициент корреляции ρij определяется rij для заданной Eij.
Таким образом, подобие форм сигналов ωi(l) и ωj(l) может быть описано как
ρij=0 ωi(l) и ωj(l)
неподобны (некоррелированы с rij=0),
0<|ρij|<1 ωi(l) и ωj(l) подобны со степенью подобия ρij
(коррелированны с rij < 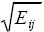 ),
),
|ρij|=1 ωi(l) и ωj(l) идентичны
(коррелированны с rij = 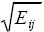 ).
).
2.3 Процедура алгоритма
Основываясь на нелинейной модели, описанной с помощью программы NETOMAC, и на корреляционном анализе, описанном выше, был создан новый алгоритм формирования динамических эквивалентов. Он выполняется во временной области и не требует какой-либо линеаризации системы. Ниже приведены наиболее значимые особенности алгоритма:
- когерентные генераторы определяются с достаточно высокой точностью благодаря применению корреляционного анализа к графикам изменения во время переходных процессов параметров генераторов;
- динамические характеристики генераторов воспроизводятся независимо от типа возмущения и расположения, т.к. для возбуждения системы используется сигнал "белый шум", обладающий равномерным распределением.
Процедура выполняется за 4-е шага:
- определение когерентных генераторов;
- агрегирование когерентных генераторов;
- создание эквивалента окружающей агрегируемые генераторы сети;
- определение параметров соответствующих эквивалентных регуляторов.
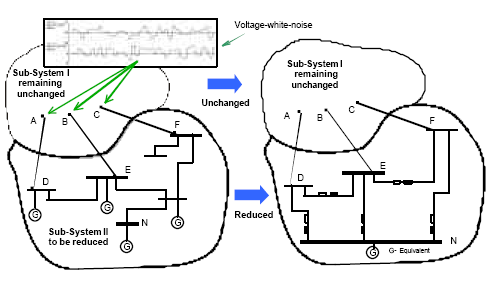
рис. 1 Схема объединенной энергосистемы
Перед началом процедуры необходимо определить следующие параметры:
- линии связи между эквивалентируемой и неэквивалентируемой частями (например, линии AD, BE, и CF на рис. 1) через которые будет вноситься возмущение;
- узел (например, узел N на рис. 1), который останется в сформированном эквиваленте;
- наименьший коэффициент корреляции в соответствие с которым будут определяться когерентные генераторы или число генераторов, которое должно остаться в эквиваленте.
Работа процедуры начинается с расчета потокораспределение в полной модели изучаемой системы, после которого автоматически запускается процедура эквивалентирования. После нахождения потокораспределения, которое определяет рабочую точку исследуемой системы, полная модель системы делится автоматически на две подсистемы как показано на рис. 1: 1-я подсистема остается неизменной, а другая будет эквивалентирована. Далее, через линии связи подсистема 2 возбуждается сигналом "белый шум".
"Белый шум" определяется как случайный сигнал νe(t) со следующими параметрами:

где

есть среднее и SVe(Ω) – спектр сигнала νe(t) [9]. Как описано в (13), "белый шум" νe(t) – это процесс с нулевым средним значением плоского спектра. Он может быть использован как источник возмущения для возбуждения системы с одинаковой интенсивностью во всем диапазоне интересуемых частот. Очевидно, что динамика генераторов, возбуждаемых "белым шумом" может быть определены независимо от типа и места приложения возмущения. Следует отметить, что 3-х фазное КЗ – это наиболее типичное возмущение, используемое для возбуждения в некоторых других методах.
(определение из Википедии http://ru.wikipedia.org/
Белый шум — стационарный шум, спектральные составляющие которого равномерно распределены по всему диапазону задействованных частот (например, шум водопада) – прим. пер.)
Далее описывается каждый выполняемый шаг:
1. Определение когерентных генераторов.
Как отмечено выше, реакция генераторов на возбуждающий сигнал моделируется во временной области. Отклонение скорости
отдельных генераторов в подсистеме 2 используется как исследуемый параметр в корреляционном анализе. Когерентные колебания
генераторов имеют коэффициент корреляции равный 1, в то время как генераторы, колеблющиеся в противофазе, имеют коэффициент
корреляции равный -1. В других случаях коэффициент корреляции находится в диапазоне между 1 и -1. Опыт показывает, что
коэффициент корреляции 0.8 можно рассматривать как пороговую величину и генераторы с большим коэффициентом корреляции
можно с достаточной точностью рассматривать как когерентные. При заданном коэффициенте корреляции когерентные генераторы
определяются автоматически благодаря использованию корреляционного анализа. Как показано на рис. 2, генераторы 1 и 2 идентифицируются
как группа когерентных генераторов с высоким коэффициентом корреляции (0.93), а генераторы 3 и 4 некогерентные, т.к. коэффициент
корреляции меньше нуля.
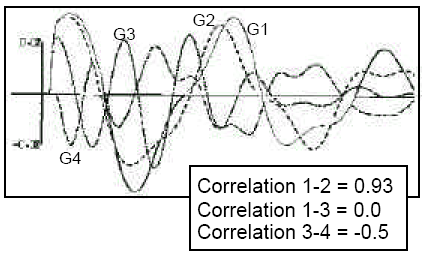
рис. 2 Определение когерентных генераторов
2. Агрегирование когерентных генераторов
Генераторы, определенные как члены одной когерентной группы агрегируются в эквивалентный генератор, подключенный к единственному
узлу (например, к узлу N на рис. 1). Таким образом, число эквивалентных генераторов определяется автоматически для заданной уставке
коэффициента корреляции. Эквивалентный генератор должен иметь подобное поведение как исходная группа генераторов с т.з. изменения
напряжения и частоты. Это может быть достигнуто вычислением сопротивлений в d- и q-осях для определенной частоты колебаний и соединением
их в параллель. Импеданс каждого генератора для агрегации определяется для следующих частот (т.к. они значимы при исследовании устойчивости):
Z``=R``+jX`` для 50 Гц (s=1) сверхпереходное сопротивление
Z`=R`+jX` для 0.5 Гц (s=0.01) переходное сопротивление
Z=R+jX для 0.001 Гц (s ~ 0) синхронное сопротивление
Эквивалентная проводимость агрегированного генератора в каждой когерентной группе определяется через (каждая проводимость
отдельного генератора в группе соединяется в параллель):

Из (15), эквивалентные параметры схемы замещения генератора, такие как xd, x`d и x``d легко вычисляются.
Момент инерции эквивалентного генератора вычисляется как сумма моментов инерций отдельных генераторов с учетом полной мощности
эквивалентного генератора:
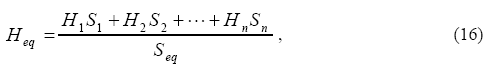
где момент инерции Hi приведен к полной мощности i-того генератора. Инъекции мощности Pi + jQi от каждого генератора складываются и дают суммарную инъекцию мощности:

Такой подход определения параметров агрегированных генераторов позволяет быть уверенным, что поведение генератора во время
сверхпереходного и переходного процессов, а так же в режиме установившегося короткого замыкания будет подобен поведению исходной
группе когерентных генераторов.
3. Создание эквивалента окружающей агрегируемые генераторы сети
Эквивалент сети создается таким образом, чтобы режим короткого замыкания и потокораспределение исходной системы оставалось
неизменным. Применяемый алгоритм создания эквивалента сети подобен приведенному в [10], в котором отдельные эквивалентные
генераторы заменяют генераторы в каждой когерентной группе, а так же сохраняется баланс. Для использования эквивалентных генераторов
без изменения заданного потокораспределения к узлу (например, узлу N на рис. 1), к которому подключается эквивалентный генератор, подключается
"идеальный" трансформатор с нулевым импедансом и комплексным коэффициентом трансформации. Включение
"идеального" трансформатора компенсирует возможный фазовый сдвиг напряжения отдельных генераторов.
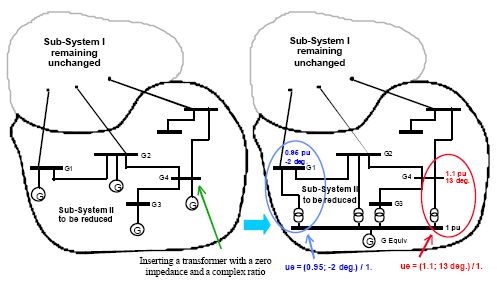
рис. 3 "Идеальный" трансформатор с нулевым импедансом и комплексным коэффициентом трансформации
4. Определение параметров соответствующих эквивалентных регуляторов
Алгоритм может выявлять различие между естественными колебаниями генераторов и воздействием регуляторов. Это реализовано
путем моделирования системы с/без соответствующих регуляторов. В случае рассматриваемых регуляторов алгоритм Гаусса-Ньютона,
описанный в [7] используется для определения параметров эквивалентных регуляторов путем подбора параметров регулятора как показано
на рис. 4. Данная процедура так же доступна в программе NETOMAC.
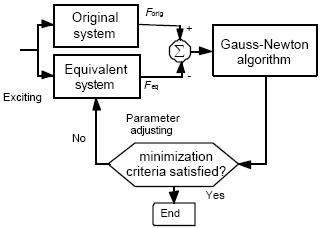
рис. 4 Процесс подбора параметров с использованием алгоритма Гаусса-Ньютона
Для подбора параметров регуляторов ко всем генераторам в когерентной группе подключаются их системы возбуждения и регуляторы скорости.
Далее они подключаются к сборной шине, которая соединена с шиной бесконечной мощности с напряжением 1 о.е. и нулевым фазовым углом.
Для возбуждения генераторов в качестве возмущения используется "белый шум", подаваемый на сборную шину. Активная и реактивная
мощности, выдаваемые генераторами в ответ на возмущение, рассматриваются как измерение оригинального сигнала Forig (см. рис. 4)
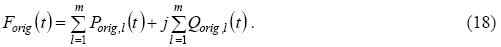
Соответствующий эквивалентный генератор с его эквивалентными регуляторами также подключается к узлу бесконечной мощности с таким же
напряжением таким же способом. В системе возбуждения и регуляторе скорости эквивалентного генератора (могут быть использованы
стандартные регуляторы IEEE или определяемые пользователем модели) выбранные параметры, такие как коэффициенты усиления, постоянные
времени получают некоторое начальное приближение и далее уточняются в ходе расчета. Такой же "белый шум" используется для
возбуждения системы. Реакция на возмущения эквивалентного генератора в виде активной и реактивной мощности используется в качестве
эквивалентных сигналов Feq для сравнения их с измеренными сигналами
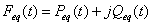 (19)
(19)
Параметры регуляторов эквивалентного генератора определяются в минимуме целевой функции
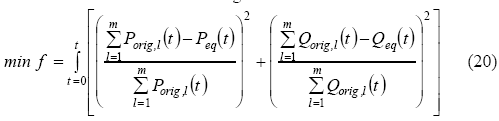
который находиться методом Гаусса-Ньютона посредством минимизации ошибки между Feq и Forig в течение всего расчетного периода времени t.
Процедура выявления динамической когерентности для формирования динамических эквивалентов работает во временной области,
базируясь на нелинейной модели исследуемой энергосистемы. В отличие от алгоритмов, основанных на линеаризованных системах,
которые достоверны только для анализа в условиях малого сигнала, данный метод позволяет получать эквивалент, отражающий нелинейное
поведение исходной системы во время больших возмущений.
3. Пример исследований
Для того, чтобы показать на практике качество эквивалентирования, была эквивалентирована сеть UCTE/CENTREL. Вычисления проводились
как в эквивалентированной, так и в полной модели. Результаты сравнения приведены в следующих параграфах. Хотя была достигнута высокая
степень эквивалентирования, результаты расчетов, проведенных в эквивалентированной модели подобны результатам расчетов динамической
устойчивости в исходной сети.
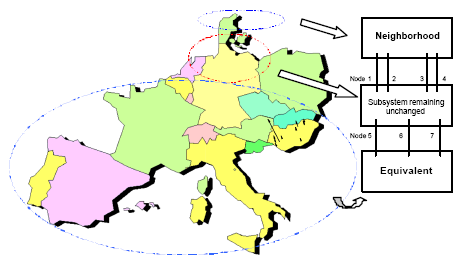
рис. 5 Схематическая иллюстрация исследуемой сети
При создании исходной модели использовался эквивалент, содержащий 400 генераторов и описывающий сеть UCTE/CENTREL, включая сеть PreussenElektra (в результате слияния PreussenElektra и Bayernwerk образовался концерн E.ON Energie – крупнейший поставщик электроэнергии в Германии, владеющий электростанциями, сетями и осуществляющий диспетчерское управление – прим. пер.) Дополнительно, была присоединена граничащая сеть. Различные части исследуемой сети схематично изображены на рис. 5.
Исходная модель разделена на три подсистемы: первая подсистема, включающая в себя район северной части Германии и западной части Дании остается без изменений (на рис. 5 "Subsystem remaining unchanged"); вторая подсистема – NORDEL, исключая западную часть Дании – так же не изменяется (на рис. 5 "Neighborhood"); третья подсистема (на рис. 5 "Equivalent"), была эквивалентирована. Оставшиеся без изменений и эквивалентированная подсистемы соединены через 7 исходных межсистемных линии.
Полная модель была эквивалентирована, используя автоматическую процедуру динамического эквивалентирования, реализованную в программе NETOMAC.
В ходе вычислений, число генераторов было снижено до 49 эквивалентных генераторов. В оставшейся без изменения подсистеме ("Subsystem
remaining unchanged") и в соседней сети ("Neighborhood") детально смоделированы 28 генераторов. В таблице 1 приведены некоторые
характеристики модели. Высокая степень эквивалентирования была выбрана в связи с тем, что в основном данная модель предполагается к
использованию для анализа динамической устойчивости.
Таблица 1 UCTE/CENTREL динамическая модель
| Параметр | Исходная модель | Эквивалентированная модель |
|---|---|---|
| Генераторы |
400
|
49+28
|
| Узлы |
2000
|
120
|
| Ветви |
6700
|
530
|
Для вычисления качества эквивалентирования с т.з. динамической устойчивости были рассчитаны максимально допустимые времена отключения
3-х фазного КЗ в 7-ми пограничных узлах в неизмененной части модели, соединяющих как граничную сеть, так и эквивалент. Названия узлов приведены
на рис. 5. Эти вычисления были проведены, используя исходную полную модель и объединенную эквивалентную модель. Оба результата были сравнены.
Относительное отклонение времени отключения КЗ приведено на рис. 6 для всех 7-ми связывающих узлов. Максимальное отклонение времени отключения
КЗ равно -4.0%, т.е. максимально допустимое время отключения КЗ, вычисленное используя эквивалент на 4.0% ниже, чем время отключения КЗ,
вычисленное по полной модели.
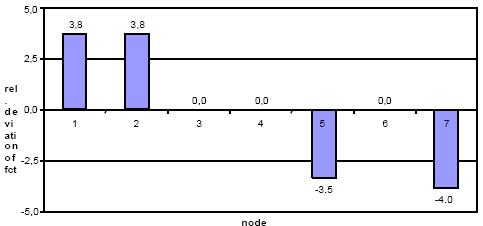
рис. 6 Относительное отклонение времени отключения КЗ
Для верификации результатов было рассчитано 3-х фазное КЗ длительностью 150 мс в узле, входящем в неизмененную часть модели как в
первоначальной полной модели, так и в объединенной эквивалентной модели. На рисунках ниже приведены активная и реактивная мощности
генераторов в неизмененной части модели. Результаты для первоначальной модели даны на рис. 7 (а), а результаты для модели с эквивалентом
показаны на рис. 7 (б).
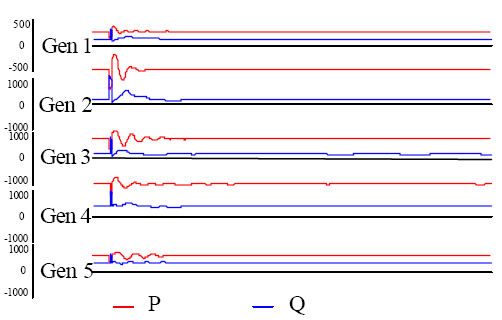
а. Первоначальная модель
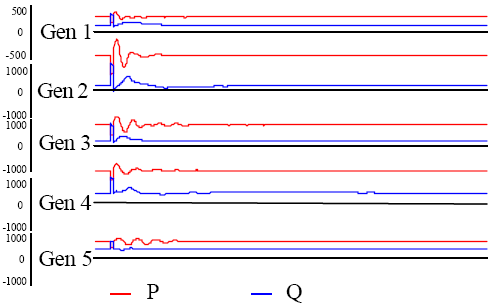
б. Модель с эквивалентом
4. Заключение
Снижение размерности расчетной модели большой энергосистемы становиться важным вопросом в условиях конкурентного рынка. В данной статье был представлен новый алгоритм создания динамических эквивалентов больших энергосистем. Под воздействием возмущения в виде "белого шума" генераторы в эквивалентируемой подсистеме возбуждаются независимо от типа и места возмущений. Когерентные генераторы во время переходного процесса идентифицируются с повышенной точностью благодаря использованию корреляционного анализа. Отличия от большинства существующих методов, значимые черты представленного в статье метода следующие:
- Эквиваленты создаются с учетом переходных процессов с повышенной точностью копирования нелинейной природы исследуемой системы;
- Вся процедура нового алгоритма включена в программу NETOMAC, в которой описана исследуемая система в нелинейном базисе и не требуется какая-либо конвертации данных.
В статье продемонстрирован пример расчетов, основанный на реальных энергосистемах. Достигнутые результаты подтверждают функциональность предлагаемого алгоритма.
Необходимым условием для выполнения эквивалентирования сети является доступность мощного инструментария и обученных инженеров, обладающих
опытом в анализе динамической устойчивости энергосистем. Включение нелинейных алгоритмов в программу NETOMAC дает эффективный инструмент
для формирования эквивалентов больших и очень больших систем в условиях конкурентного рынка.
5. Литература
[1] R.J. Newell, M.D. Risan, L. Allen, K.S. Rao, D.L. Stuehm, "Utility experience with coherency-based dynamics equivalents of very large systems," IEEE Transaction
on Power Apparatus and Systems, Vol. 104, No. 11, November 1985, pp. 3056 – 3063
[2] G. Troullions, J. Dorsey, H. Wong, and J. Myers, "Reducing the order of very large power system models," IEEE Transaction on Power Systems, Vol. 3, No. 1,
February 1988, pp. 127 – 133
[3] J. H. Chow, R. Galarza, P. Accari, W. W. Price, "Inertial and slow coherency aggregation algorithms for power system dynamic model reduction," IEEE
Transaction on Power Systems, Vol. 10, No. 2, May 1995, pp. 680-685
[4] L. Wang, M. Klein, S. Yirga, P. Kundur, "Dynamic reduction of large power system for stability studies," IEEE Transaction on Power Systems, Vol.
12, No. 2, May 1997, pp. 889 - 895
[5] B. Kulicke, "NETOMAC Digital Program for Simulating Electromechanical and Electromagnetic Transient Phenomena in AC System,"
Elektrizitätswirtschaft Heft 1 (1979), S. 18-23
[6] X. Lei, E. Lerch, D. Povh, O. Ruhle, "A large integrated power system software package NETOMAC," POWERCON`98, International
Conference on Power System Technology, Beijing, China, 1998, pp. 17 – 22
[7] X. Lei, D. Povh, E. Lerch, B. Kulicke, "Optimization – a new tool in simulation program system," IEEE Transaction on Power Systems,
Vol. 12, No. 2, May 1997, pp. 598 – 604
[8] M. A. Pei, R. P. Adgaonkar, "Identification of coherent generators using weighed eigenvectors," IEEE Paper A79-022-5, presented at
PE Winter Meeting, New York, 1979
[9] A. Papoulis, "Probability, Random Variables and Stochastic Process," 2-nd ed. New York: McGraw-Hill, 1984.
[10] W. F. Tinny, J. M. Bright, "Adaptive reduction for power flow equivalent," IEEE Transaction on Power Systems, Vol. PWRS-2, May 1987, pp. 351 – 360
Биографии:
Xianzhang Lei родился в Китае. Получил степень бакалавра в Zhejiang University, Китай, степень магистра и доктора электротехники в
Technical University of Berlin, Германия в 1982, 1987 и 1992 годах соответственно. С 1994 года является senior manager in the Power Transmission
and Distribution Group at Siemens в Эрланде, Германия. Он является junction-professor в нескольких университетах КНР.
Olaf U. Ruhle родился в Германии в 1965 году. Получил диплом инженера и степень доктора электротехники в Technical University of Berlin
в 1990 и 1994 годах соответственно. С 1993 года является членом Power Transmission and Distribution Group and the system planning and consulting
department at Siemens в Эрланде, Германия. Его работа связана с устойчивостью энергосистем, динамикой многомашинных систем, вопросами
управления, оптимизации и идентификации электроэнергетических систем. Он отвечает за поддержку программы NETOMAC, продажи и обучение во всем мире.
Bernd Kulicke родился в Wernigerode, Германия. Получил степень магистра в Technical University of Berlin в 1970 году и степень доктора в
University of Darmstadt в 1975 году. С 1970 по 1983 года работал в Siemens AG и отвечал за развитие программы NETOMAC, где в основном учувствовал
в исследовательских работах, связанных с изучением свойств энергосистем, включая электромеханические и электромагнитные переходные процессы
и вопросы устойчивости. С 1984 года является профессором и руководителем департамента High Voltage Power Engineering в Technical University of Berlin, Германия.
Сергей Мотовилов