В. Л. Прихно, канд. техн. наук (Ин-т электродинамики НАН Украины, Киев)
Ю.В. Масайлов (Объединенное диспетчерское управление энергосистемами Урала)
ОЦЕНИВАНИЕ РЕЖИМОВ ЭНЕРГОСИСТЕМ ДЛЯ ИСПОЛЬЗОВАНИЯ В СОСТАВЕ СИСТЕМЫ ЦЕНТРАЛИЗОВАННОЙ ПРОТИВОАВАРИЙНОЙ АВТОМАТИКИ
(Сборник докладов II Всероссийской научно-технической конференции. – Екатеринбург: Изд-во ГОУ ВПО УГТУ-УПИ, 2004. - С. 206-210.)
В настоящее время в стадии разработки находится система централизованной противоаварийной автоматика (ЦПА) для объединенных энергосистем Урала, Средней Волги и Северного Кавказа. В первых двух новая разработка должна заменить существующие, но морально и физически устаревшие системы, находящиеся в эксплуатации более 10 лет. Очевидно, при реализации данного проекта должен быть обобщен опыт эксплуатации существующих систем.
Составной частью ЦПА является программа оценивания текущего режима энергообъединения на основе телеметрической информации. В результате ее работы формируется математическая модель существующего режима, которая затем проверяется на устойчивость при возникновении тех или иных возмущений. От адекватности модели существующему режиму зависит точность решений, связанных с проверкой устойчивости и расчетом дозировок управляющих воздействий.
В целом положительный опыт эксплуатации программы оценивания состояния в составе существующих комплексов ЦПА позволил определить и наиболее слабые места в ее работе. Проблемы возникают, как правило, в случаях одновременного возникновения нескольких грубых ошибок или отказов в системе сбора телеметрической информации. При разработке новой программы оценивания ставится цель повышения надежности ее работы и точности результатов.
Основные недостатки существующей программы оценивания состояния касаются, прежде всего, следующих моментов:
- неоптимальные решения при выборе способа компенсации дефицита реальных телеизмерений при общей ненаблюдаемости режима в связи с отказами некоторых измерительных каналов;
- отсутствие программных средств для проверки состояния ветвей схемы замещения (включено – отключено) и, как следствие, к неправильным решениям при поиске и отбраковке ошибочных измерений;
- невозможность использования резервных измерений, частично дублирующих основные измерения;
- отсутствие контроля уровней рассчитываемых напряжений, приводящее в некоторых случаях к получению оценок с неправдоподобными напряжениями в узлах расчетной схемы (может иметь место при наличии в измерениях не выявленных грубых ошибок в связи с отсутствием избыточности телеизмерений);
- отсутствие блока самодиагностики, функцией которого было бы принятие окончательных решений о целесообразности дальнейшего использования результатов в случаях, когда с формальной математической точки зрения вычислительный процесс завершился успешно.
По мнению авторов, наиболее эффективные алгоритмы решения задачи оценивания состояния могут быть реализованы на основе методов наименьших
взвешенных квадратов и наименьших модулей. Первый подход предполагает минимизацию целевой функции (1):
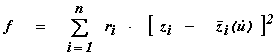 (1)
(1)где n - число измерений;
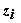 - значение i-го измерения;
- значение i-го измерения; 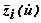 - функция, отражающая зависимость между i-м измерением и независимыми параметрами, в качестве которых выступают модули и фазы напряжений в узлах
схемы замещения;
- функция, отражающая зависимость между i-м измерением и независимыми параметрами, в качестве которых выступают модули и фазы напряжений в узлах
схемы замещения; 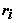 - весовой коэффициент, характеризующий точность i-го измерения.
- весовой коэффициент, характеризующий точность i-го измерения.
При втором подходе оценки параметров режима получаются в результате минимизации целевой функции (2):
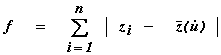 (2)
(2)Оптимизация обеих целевых функций проводится с учетом ограничений на диапазон изменения оцениваемых параметров. При невысокой избыточности измерений учет ограничений позволяет снизить влияние ошибок в измерениях, а в ряде случаев и более обоснованно решать вопрос о том, какие измерения содержат грубые ошибки.
В связи с тем, что зависимости 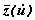 нелинейные, как в первом, так и во втором случаях минимизация целевой
функции осуществляется в виде итерационного процесса. При использовании целевой функции (1) последняя на каждой итерации заменяется квадратичной
аппроксимацией и для ее оптимизации решается задача квадратичного программирования. В случае использования целевой функции (2) линеаризация
зависимостей на каждой итерации приводит к необходимости решения задачи линейного программирования. Поскольку в традиционной постановке не
предполагается использование в целевой функции абсолютных величин, базовый алгоритм решения задачи линейного программирования, в качестве
которого используется симплекс – метод, должен быть существенно модифицирован.
нелинейные, как в первом, так и во втором случаях минимизация целевой
функции осуществляется в виде итерационного процесса. При использовании целевой функции (1) последняя на каждой итерации заменяется квадратичной
аппроксимацией и для ее оптимизации решается задача квадратичного программирования. В случае использования целевой функции (2) линеаризация
зависимостей на каждой итерации приводит к необходимости решения задачи линейного программирования. Поскольку в традиционной постановке не
предполагается использование в целевой функции абсолютных величин, базовый алгоритм решения задачи линейного программирования, в качестве
которого используется симплекс – метод, должен быть существенно модифицирован.
В версии программы оценивания состояния, функционирующей в составе существующей ЦПА, в качестве основы алгоритма используется метод, предполагающий минимизацию целевой функции (1). Однако более поздние исследования позволили сделать вывод о том, что второй подход, основанный на минимизации функции (2), имеет ряд существенных преимуществ, среди которых в первую очередь необходимо выделить следующие:
- практически автоматически решаются вопросы проверки наблюдаемости режимов и отбраковки грубых ошибок в измерениях;
- проще реализуется учет ограничений на возможный диапазон изменения рассчитываемых параметров, в том числе – более надежно (с математической точки зрения) осуществляется снятие ограничений, если необходимость их использования на некотором этапе отпадает;
- более просто может быть реализована методика проверки правильности задания состояния топологии сети на основе телесигналов.
Основной недостаток алгоритма, основанного на минимизации целевой функции (2) состоит в возможности получения расходящегося итерационного процесса в случае, если измерения и ограничения, выбранные в качестве базисных, образуют несовместную систему нелинейных уравнений.
При использовании в качестве основы алгоритма метода взвешенных наименьших квадратов вопросы отбраковки ошибочных измерений и учета ограничений решаются сложнее, чем при использовании подхода, основанного на минимизации функции (2), однако к преимуществам первого следует отнести следующие:
- возможность получения оценок, максимально приближенных к измерениям даже в случаях, когда нелинейная система несовместна;
- результат расчета с использованием функции (1) наилучшим образом соответствует всей совокупности измерений, а не только тем, которые попали в число базисных.
Необходимо отметить, что для получения надежных оценок требуется модификация алгоритма, предполагающая коррекцию матрицы вторых производных (матрицы Гессе), в случаях, если на некоторой итерации она теряет положительную определенность.
После того, как был приобретен опыт расчетов с использованием алгоритмов, основанных на минимизации целевых функций (1) и (2) и стали очевидны как их сильные стороны, так и недостатки, была предпринята попытка разработать методику, основанную на сочетании подходов, с целью использования преимуществ каждого из них.
В разрабатываемой новой версии программы оценивания состояния реализуется методика, включающая следующие этапы:
- Производится предварительный контроль качества измерений и устраняются грубые ошибки путем проверки простых логических соотношений, в том числе: соответствия величин потоков активных и реактивных мощностей по концам ветвей; соблюдения с заданной точностью балансов мощностей в узлах; соответствия потоков реактивных мощностей уровням напряжений по концам ветвей и ряда других. В результате проверки отбраковывается часть измерений, а некоторые измерения получают признаки, характеризующие степень доверия к ним. Так, например, условно достоверными можно считать измерения потоков мощности по концам ветвей, если они хорошо согласуются между собой. Признаки достоверности используются в дальнейшем при формировании исходного базисного состава измерений при минимизации целевой функции (2).
- Выполняется анализ наблюдаемости режима и определяется минимальный состав псевдоизмерений из заранее определенного списка в случае, если наблюдаемость по располагаемым измерениям не обеспечивается. Оценивается состав рассчитываемых параметров режима, на которые оказывают влияние введенные псевдозамеры, т. е. определяются районы, ненаблюдаемые по реальным измерениям.
- Производится минимизация целевой функции по методу взвешенных наименьших квадратов (1). При этом учитывается вся совокупность замеров, за исключением тех, которые признаны ошибочными на первом этапе расчета. В процессе минимизации последовательно учитываются нарушенные ограничения. Учет каждого нового ограничения реализуется путем введения дополнительного штрафного слагаемого и связан с коррекцией решения путем пересчета вектора – градиента и матрицы Гессе, которые соответствуют аппроксимации на очередной итерации.
- В точке оптимума выполняется проверка правильности задания топологии. Решение об изменении состояния ветви принимается в случаях, когда потокораспределение при измененной топологии обеспечивает существенное снижение целевой функции. Очевидно, набор вариантов для проверки должен быть ограничен. В связи с этим под проверку попадают ветви, входящие в районы, расчетные параметры для которых существенно отличаются от измеренных. При этом оценивается эффективность включения отключенных ветвей и отключения включенных, если измеренные потоки по этим ветвям близки к нулю.
- В точке оптимума выполняется линеаризация зависимостей и решается задача линейного программирования. Минимизация целевой функции (2) осуществляется последовательным улучшением состава базисных измерений. При этом учитываются ограничения на возможный диапазон изменения расчетных величин. В процессе оптимизации возможен как учет новых ограничений, так и снятие ограничений при определенных условиях. Уравнения, соответствующие небазисным измерениям, образуют контрольную систему. Если по некоторым контрольным уравнениям отклонения превышают заданные пороговые величины, они признаются ошибочными.
- Завершается минимизация нелинейной целевой функции взвешенных наименьших квадратов (1). При этом используются результаты, полученные на предыдущем этапе, т. е. сохраняется состав активных ограничений и не учитываются измерения, ранее признанные ошибочными.
Разработанная программа оценивания состояния работает под управлением диспетчера ЦПА и взаимодействует с базой данных через специализированный программный интерфейс. Сервисная поддержка обеспечивается как специальными средствами ЦПА, так и средствами программного комплекса КОСМОС.
- Ф. Гилл, У. Мюррей, М. Райт. Практическая оптимизация. – М.: Мир, 1985. –509 c.
- Муртаф Б. Современное линейное программирование. – М.: Мир, 1984. –224c.