Виталий Леонидович Прихно
УСТРАНЕНИЕ ОШИБОК В ЗАДАНИИ ТОПОЛОГИИ СЕТИ ПРИ ОЦЕНИВАНИИ РЕЖИМОВ ЭНЕРГОСИСТЕМ
(Тр. Института электродинамики НАНУ, №2(14), Киев, 2006. С. 26-27.)
Большой опыт внедрения программы оценивания состояния для расчетов режимов энергосистем и энергообъединений убеждает в том, что в настоящее время наиболее слабым звеном при формировании модели электрического режима является наличие ошибок в телесигналах, в результате чего на этапе синтеза формируется неверное описание расчетной схемы. К наиболее распространенным относятся ошибки в определении состояния ветвей (включена или отключена). До последнего времени задача уточнения состояния топологии в рамках оценивания режимов не ставилась и не решалась.
Основная проблема идентификации ошибок в задании топологии сети заключается в необходимости отделить их от ошибок в измерениях. Наличие и тех, и других существенно искажает результат оценивания. При этом в обоих случаях в районах, близких к источнику ошибки, наблюдаются значительные отклонения между измеренными и расчетными величинами. Очевидно, чтобы констатировать факт ошибки в задании топологии расчетной схемы, необходимо определить элемент, изменение состояния которого существенно уменьшает число неприемлемых отклонений между измеренными и рассчитанными параметрами в возмущенном районе. Если изменение состояния приводит к большему выигрышу, чем устранение любого из замеров, то можно предположить, что ошибочно задано состояние элемента расчетной схемы, а не какое-либо измерение. Выигрыш целесообразно оценивать как по величине снижения значения целевой функции оценивания, так и по числу неприемлемых отклонений между измеренными и рассчитанными параметрами.
В результате большого числа экспериментов, выполненных на основе реальных математических моделей режимов энергосистем и энергообъединений,
разработана методика решения задачи. В ее основе лежит целенаправленный перебор вариантов изменения состоянии отдельных элементов. Задача
решается в три этапа, причем после каждого этапа сокращается число ветвей, состояние которых уточняется. Первый этап заключается в безусловной минимизации
целевой функции оценивания состояния, соответствующей критерию наименьших взвешенных квадратов:
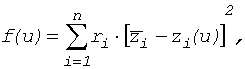 (1)
(1)где
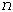 - общее число замеров;
- общее число замеров;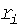 - весовой коэффициент, учитывающий точность i-го измерения;
- весовой коэффициент, учитывающий точность i-го измерения;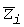 - величина i-го измерения;
- величина i-го измерения;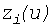 - функция, отражающая связь между параметром режима, соответствующим
i-му измерению, и независимыми переменными u, в качестве которых выступают модули и фазы напряжений в узлах схемы.
- функция, отражающая связь между параметром режима, соответствующим
i-му измерению, и независимыми переменными u, в качестве которых выступают модули и фазы напряжений в узлах схемы.
Очевидно, ставить под сомнение состояние большинства ветвей расчетной схемы не целесообразно. Если после минимизации функции (1) оказывается, что расчетные величины потоков мощности по некоторым ветвям несущественно отличаются от соответствующих измерений, то маловероятно, что состояние этих ветвей задано ошибочно. Первый этап идентификации ошибок в топологии сети завершается формированием списка линий, состояние которых признается сомнительным. В этот список попадают ветви, по которым либо отсутствуют измерения потоков мощности, либо расчетные величины потоков значительно отличаются от измеренных.
Прежде, чем проверять возможность включения или отключения ветви необходимо убедиться, что планируемое изменение состояния не приведет к потере наблюдаемости. Задача второго этапа состоит в удалении из списка ветвей сомнительного состояния тех, отключение которых приводит к потере наблюдаемости. Для проверки возможности изменения состояния той или иной ветви с точки зрения сохранения наблюдаемости предложен следующий подход. По сути, отключение ветви эквивалентно изменению ее проводимости от некоторой величины, соответствующей ее параметрам, до нуля. Алгоритм предлагает поочередное расширение числа независимых переменных оценивания на одну переменную, путем добавления к модулям и фазам напряжений узлов коэффициента изменения проводимости тестируемой ветви. Последний изменяется в диапазоне от 1 (ветвь включена) до 0 (ветвь отключена). При расчете параметров режима и производных на данный коэффициент умножается активная и реактивная проводимость тестируемой ветви. Для наблюдаемой системы характерна хорошая обусловленность матрицы Гессе (матрицы вторых производных квадратичной аппроксимации целевой функции). Если расширение числа переменных приводит к тому, что матрица Гессе становится вырожденной, это свидетельствует о потере наблюдаемости. В таком случае следует отказаться от уточнения состояния очередной ветви и вывести ее из списка ветвей сомнительного состояния.
Третий, уточняющий, этап расчета связан с проверкой возможных решений при измененном состоянии сомнительных ветвей. Проверка осуществляется путем коррекции некоторого базового решения, соответствующего точке безусловного минимума целевой функции (1). Если проанализировать структуру матрицы Гессе, то при включении или отключении одной из ветвей она меняется незначительно. Поскольку целевая функция (1) является суммой квадратов отклонений между измеренными и расчетными величинами, то и матрица Гессе определяется суммированием квадратичных аппроксимаций отклонений каждого из измерений. Поэтому, изменение состояния той или иной ветви сказывается лишь на те составляющие, которые соответствуют либо измерениям потоков мощности по тестируемой ветви, либо измерениям мощностей в узлах схемы, к которым примыкает тестируемая ветвь. При включении или отключении некоторой ветви изменяются лишь четыре столбца и четыре строки, соответствующие взаимным частным производным модулей и фаз напряжений узлов, которые эту ветвь ограничивают. Учитывая сказанное, самая трудоемкая операция обращения матрицы Гессе может быть заменена процедурой коррекции обратной матрицы. Перебор вариантов изменения состояния ветвей, оставшихся в списке сомнительного состояния, дает приемлемые результаты как по точности идентификации, так и по быстродействию.
Испытания предложенного алгоритма подтвердили его эффективность. Программа оценивания состояния, включающая проверку состояния ветвей и реакторов включена в состав программного комплекса КОСМОС и внедрена и эксплуатируется в Объединенном диспетчерском управлении энергосистемами Урала.
 |
Прихно Виталий Леонидович Старший научный сотрудник отдела №3 ИЭД НАН Украины. Родился в 1951 г. В 1973 г. Закончил Запорожский машиностроительный институт. В 1983 г. защитил кандидатскую диссертацию по специальности «Электрические станции (электрическая часть), сети и системы и управление ими». Основные научные интересы: разработка методик, алгоритмов и программ для оперативных расчетов режимов энергосистем на основе телеметрической информации. |