| Шпаргалка режимщика | ||||||||||||||||||||||
Модели элементов для расчета динамики |
||||||||||||||||||||||
Синхронная машинаМоделирование синхронной машины (СМ) подразумевает под собой нахождение закона изменения вектора ЭДС
Угол вектора ЭДС 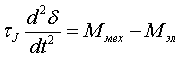 (1) (1)
где d2δ/dt2 - угловое ускорение; τJ - механическая постоянная инерции всего агрегата; Ммех - механический момент на валу синхронной машины; Мэл - электромагнитный момент. Для учета тех составляющие демпфирующего момента, которые в силу каких-либо допущений не отражаются
через механический или электромагнитный момент Мэл, в уравнение (1) добавляют слагаемое, пропорциональное
скольжению и коэффициенту демпфирования. При этом существует два варианта: использовать скольжение ротора
относительно синхронной оси (уравнение 2а) или скольжение ротора относительно вектора напряжения на зажимах
машины (уравнение 2б): 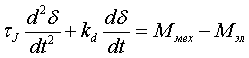 (2a) (2a)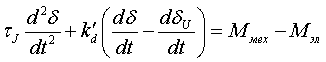 (2б) (2б)
где dδ/dt - скольжение ротора относительно синхронной оси; (dδ/dt-dδU/dt) - скольжение ротора относительно вектора напряжения на зажимах машины; kd и k`d - эмпирические коэффициенты. Оба способа приближенны, но второй может давать несколько меньшие погрешности. При одинаковых эффектах демпфирования k`d>kd. Механическая постоянная инерции τJ, которая входит в уравнение движения, равна времени, в течение которого частота вращения
изменяется на 100 % под действием приложенного к валу постоянного результирующего момента, равного номинальному моменту машины.
Численные значения τJ зависят от того, в каких единицах выполняются расчеты. Если уравнение движения записано в относительных
единицах, где за базисную мощность Sбаз принята номинальная кажущаяся мощность машины
Sном, то: 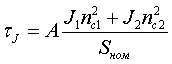 (3а) (3а)
Если же Sбаз=Рном, то: 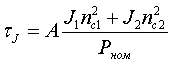 (3б) (3б)
где J1, J2 - моменты инерции генератора и турбины или двигателя и приводимого во вращение механизма; nc1, nc2 - их синхронные частоты вращения, об/мин (nc1 ≠ nc2, если двигатель работает с редуктором); Sном - номинальная кажущаяся мощность машины, МВА; Pном - номинальная активная мощность машины, МВт; Коэффициент А зависит от того, в каких единицах задан момент инерции:
Механический момент на валу синхронных двигателей обычно представляют в виде квадратичной зависимости от частоты вращения, например в
простейшем виде: 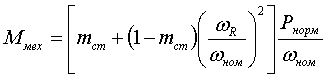 (4) (4)
где mст - статический момент сопротивления, отн. ед.; Рнорм - активная мощность в исходном режиме, отн. ед. Выбор рациональной модели (системы уравнений) для определения модуля ЭДС Используемые в настоящее время модели с переменной ЭДС обладают рядом особенностей и содержат в себе следующие допущения:
Задача моделирования регуляторов СМ заключается в представлении их влияния на вектор ЭДС Модель РС тесно связана с моделью турбины, а так же котла и его систем регулирования. Назначение модели РС - отобразить изменение мощности турбины во время переходного процесса. Детализация модели РС во многом зависит от решаемых задач. Например, если рассматриваются только первый - второй цикл качаний, то РС можно не учитывать и принять РТ=const. Если же рассматривается переходный процесс в котором с момента изменения частоты проходит до 5-10 с, то учет РС необходим, но при этом допустимо предположить, что давление пара перед турбиной постоянно и соответственно не учитывать модель котла и работу его регуляторов. При выполнении более длительных расчетов необходимо учитывать работу и РС турбины и изменение давления пара перед турбиной (т.е. модель котла и его регуляторов). Дополнительно, в модели гидротурбины может быть учтено явление гидроудара. При моделировании регулирования возбуждения необходимо учитывать регулятор и возбудитель. Исходя из решаемых задач может потребоваться так же моделирование и ряда технологических защит: ОМВ и ограничитель тока ротора. Принятый во многих промышленных программах подход к моделированию регуляторов, как правило, заключается в использовании неких простейших моделей, позволяющих, по мнению авторов, качественно правильно воспроизвести процесс, однако при этом численные значения исходных данных отличаются от значений, присутствующих на реальных объектах, а иногда отличается и состав исходной информации. При этом единственным способом произвести корректную настройку регуляторов является проведение ряда "настроечных" расчетов для подгонки получаемых результатов под реальные осциллограммы. Однако существует ряд программ (к сожалению, пока только иностранных), в которых пользователю дана возможность самостоятельно создавать регуляторы из
типовых блоков. Таким образом у технолога появляется возможность создать модель регулятора именно с такой детализацией, какая требуется ему для
решения его задач и которую он способен обеспечить исходными данными, вплоть до точной копии объекта моделирования. Например, модель турбины
можно представить в виде одного диф.уравнения, а можно в виде восьми диф.уравнений. В качестве примера подобного подхода можно привести работы
ОАО "НИИПТ", специалисты которого в среде программы
EUROSTAG используют созданные ими точные математические модели регуляторов возбуждения,
позволяющие использовать в расчетах фактические настройки АРВ без проведения каких-либо дополнительных настроечных расчетов.
Модель нагрузкиТочность, с которой требуется представлять нагрузку определяется, как всегда, решаемой задачей. Для большинства расчетов электромеханических переходных процессов в энергосистемах, как правило, достаточно представлять нагрузку в виде зависимости от напряжения в узле (СХН):Sн=f(U) При этом наиболее широкое применение нашла квадратичная зависимость нагрузки от напряжения (Zн=const, см. статью про подготовку исходных данных для УР). Она используется или сразу после начала расчета, либо после достижения напряжением в узле некоторой наперед заданной величины. Применение подобного подхода для всех узлов исключает возможность учитывать в расчетах динамические свойства нагрузки, так как величина нагрузки определяется только текущим уровнем напряжения, что не корректно. При резких изменениях напряжения (возникновение и отключение КЗ, коммутации в сети) скольжение асинхронных двигателей и углы δ синхронных двигателей не успевают прийти к своим установившимся значениям. Особенно большие погрешности появляются при самозапуске двигателей. Поэтому СХН при расчетах переходных процессов применимы только для тех узлов, где не происходит глубоких изменений напряжения (либо нет двигательной нагрузки). В общем виде динамическая модель нагрузки состоит из моделей асинхронного и синхронного двигателей, а так же из модели статических электроприемников (бытовая нагрузка, электропечи и пр.). Модель асинхронного двигателя будет описана ниже. Для моделирования синхронного двигателя необходимо использовать модель синхронной машины, описанную ранее. Для представления статических электроприемников необходимо применять СХН (как правило Zн=const). Модель асинхронного двигателя может быть реализована в двух видах: с учетом и без учета электромагнитных переходных процессов. В первом случае уравнения близки к тем, которыми описывается синхронная машина: в каждой оси ротора двигателя учитывается по одному или по два демпферных контура. В этой модели активная и реактивная мощности двигателя Pа.д. и Qа.д. зависят от напряжения, скольжения двигателя и от производной скольжения, т.е. от ускорения. Модели второго вида содержат упрощенные уравнения, в которых Pа.д.=f1(U,s), Qа.д.=f2(U,s), и не зависят от ds/dt. Разница между этими моделями проявляется только при наличии значительных ускорений, главным образом в конце самозапуска, когда вращающий момент двигателя при U≈Uном превышает номинальное значение примерно вдвое. Эти различия не являются решающими и мало влияют на точность расчетов, тем более что в переходных процессах участвуют не единичные двигатели, а их большие совокупности, когда отдельные детали процессов сглаживаются. Кроме того, при использовании упрощенной модели требуется меньше исходных данных. В модели асинхронного двигателя, составленной без учета электромагнитных переходных процессов, содержаться четыре уравнения: уравнение движения, уравнения для Pа.д. и Qа.д. и зависимость момента сопротивления на валу двигателя от его скольжения sR. Уравнение движения: 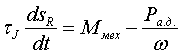 (7) (7)уравнение для активной мощности: 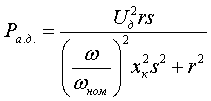 (8) (8)где Uд - напряжение на зажимах двигателя; ω - частота напряжения на зажимах двигателя; s - скольжение ротора относительно вектора напряжения. Для асинхронных двигателей скольжения sR и s считают положительными, если частота вращения ниже синхронной: 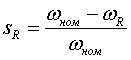 (9а) (9а)
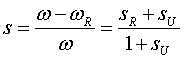 (9б) (9б)Сопротивление короткого замыкания xк и активное сопротивление ротора r достаточно сложным образом
зависят от частоты тока в роторе, равной sω. Если принять значения xк и r постоянными и включить
их в число исходных данных, то при больших s мощности Pа.д. и Qа.д. будут получены со
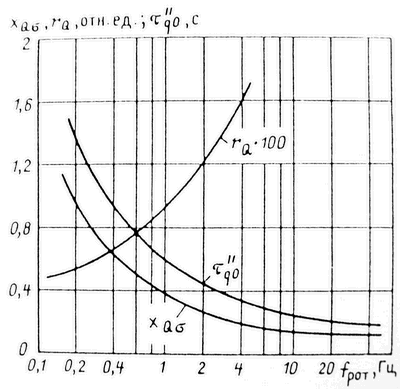
значительными ошибками. Достаточно правильные результаты расчетов получаются в том случае, если пользоваться зависимостями
xк(s) и r(s), показанными на рисунке: 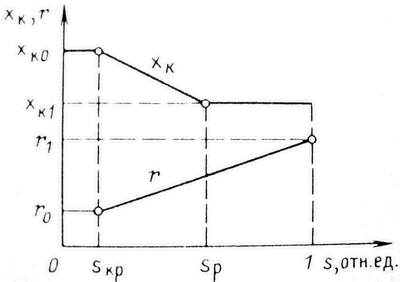 рис. 3 Приближенный учет зависимостей параметров асинхронного двигателя от частоты токов в роторе. Тогда в число исходных данных включаются значения xк0, хк1, r0, r1, sр (или другие величины, которые позволяют вычислить эти значения); критическое скольжение sкр определяется как r0/xк0. Реактивная мощность двигателя описывается выражением: 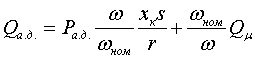 (10) (10)где Qμ - реактивная мощность намагничивания. Она зависит от Uд достаточно сложным образом из-за нелинейности характеристики холостого хода. Для Qμ используются различные приближенные выражения вида: 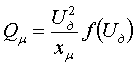 (11) (11)где xμ - сопротивление намагничивания при номинальном напряжении. Функция f(Uд) служит для отображения нелинейности характеристики холостого хода, например: 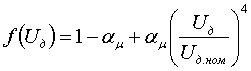 (12) (12)или 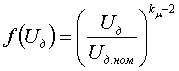 (13) (13)без учета нелинейности f(Uд)=1, αμ=0, kμ=2. Момент сопротивления на валу двигателя обычно представляют зависимостью Mмех=f(sR): 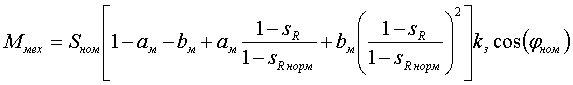 (14) (14)или 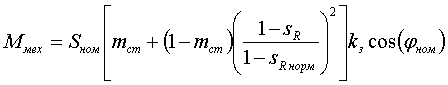 (15) (15)где mст=1-aм-bм - статический момент сопротивления, т.е. момент сопротивления при нулевой частоте вращения, отн. ед.; sR норм - скольжение ротора двигателя в нормальном (исходном) режиме; kз - коэффициент загрузки, kз=Рраб/Рном. Имеются две возможности задания параметров асинхронного двигателя: с использованием каталожных данных или параметров схемы его замещения. В обоих случаях задаются Рном, Uном, cos(φном), скольжение sр (см. рис. 3), kμ (или αμ), kз, mст (или aм, bм), τJ. В первом случае к этим параметрам добавляются значения mmax=Mmax/Mном, mп=Mпуск/Mном, iп=Iпуск/Iном и номинальное скольжение sном; во втором - xк0, xк1, xμ, r0, r1. В расчетах энергосистем обычно фигурирует не напряжение Uд на зажимах двигателя [см. выражения (8) - (11)], а напряжение в узле примыкания нагрузки. Между этим узлом и шинами электроустановок обычно имеются трансформаторы и линии, не учитываемые в расчетных схемах. При эквивалентировании асинхронной нагрузки эквивалентный (моделируемый) асинхронный двигатель считают подключенным непосредственно к узлу примыкания нагрузки. Это приводит к двум следствиям:
Параметры обобщенного асинхронного двигателя таковы: cos(φном)=0.8, mmax=1.7, mп=0.73, iп=4.1, sном=2 %, sр=70 %, kμ=4 (или αμ=0.5), kз=0.7, mст=0.5 (или aм=0, bм=0.5); механическая постоянная инерции τJ, соответствующая формуле (3а), для кратковременных возмущений принимается равной 0.8 с, если же двигатели в расчетах глубоко тормозятся, то τJ=0.6 c. Указанным данным соответствуют следующие параметры схемы замещения, отн. ед.: xк0=0.368, xк1=0.266, xμ=2.95, r0=0.0226, r1=0.0424. Уравнения связи между каталожными данными и параметрами схемы замещения следующие: 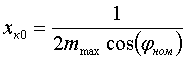 (19) (19)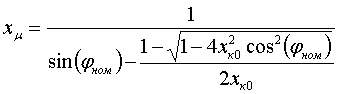 (20) (20)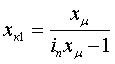 (21) (21)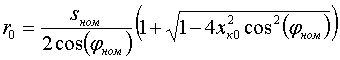 (22) (22)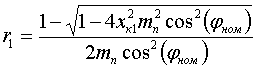 (23) (23)При проведении расчетов, связанных с самозапуском , нужно обратить внимание на то, что при неизменной
длительности перерыва питания продолжительность самозапуска часто оказывается больше в тех случаях, когда
τJ двигателей меньше, а не наоборот. Это связано с нелинейностью асинхронной характеристики
двигателя: его избыточный момент М-Ммех обычно тем меньше, чем больше скольжение двигателя
по сравнению с sкр к концу перерыва питания. Поэтому двигатель с малой механической постоянной
инерции после достаточно длительного перерыва питания имеет сравнительно малый избыточный момент, его самозапуск
занимает значительный промежуток времени. Наоборот, при большой механической постоянной инерции двигатель
тормозится мало и в начале самозапуска имеет скольжение, близкое к критическому, и относительно большой
избыточный момент - процесс его самозапуска будет кратковременным. Так, для одной группы асинхронных двигателей
при перерыве питания длительностью 1 с получена следующая зависимость продолжительности самозапуска от τJ:
При моделировании нагрузки нередко возникает вопрос: поскольку определить большинство ее параметров применительно к каждому моделируемому узлу практически невозможно и остается использовать тем или иным образом усредненные их значения, не возникнут ли при этом такие погрешности, из-за которых моделирование асинхронной нагрузки окажется вообще неоправданным? Асинхронная нагрузка при всех своих различиях в деталях, зависящих в основном от вида производства, характеризуется рядом общих свойств.
Главное из них состоит в том, что двигатели, затормозившиеся в результате снижения напряжения, в течение некоторого времени (при самозапуске)
потребляют повышенные токи. Нагрузка, описанная СХН, разумеется, не дает этого эффекта. Поэтому погрешности, вызванные отказом от уравнений
асинхронного двигателя и заменой их на СХН, много больше тех погрешностей, которые обусловлены неточностью задания параметров. Необходимость
в уточнении параметров эквивалентного двигателя возникает в редких случаях; этот вопрос детально описан в [1] в разделе, посвященном выполнению
расчетов устойчивости нагрузки применительно к системам электроснабжения крупных промышленных предприятий.
|
||||||||||||||||||||||
последние изменения 08.10.06 Сергей Мотовилов |
 .
.
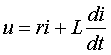 вместо
вместо
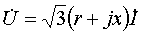 ), что существенно усложнило бы программу и замедлило бы расчеты. Кроме того, в
некоторых случаях при решении уравнений возникали бы колебания электромагнитного момента с частотой около 100 Гц. Это потребовало бы
значительного уменьшения шага интегрирования, т.е. привело бы к дополнительному замедлению расчетов и накоплению погрешностей,
обусловленных приближенностью численных методов интегрирования.
), что существенно усложнило бы программу и замедлило бы расчеты. Кроме того, в
некоторых случаях при решении уравнений возникали бы колебания электромагнитного момента с частотой около 100 Гц. Это потребовало бы
значительного уменьшения шага интегрирования, т.е. привело бы к дополнительному замедлению расчетов и накоплению погрешностей,
обусловленных приближенностью численных методов интегрирования.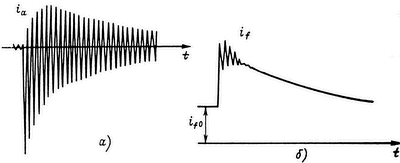
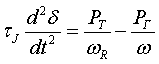 (5)
(5)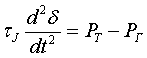 (6)
(6)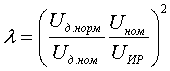 (16)
(16)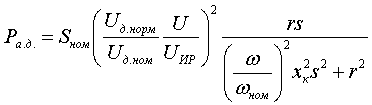 (17)
(17)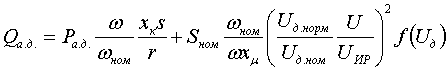 (18)
(18)